Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1991 AIME Problems/Problem 4"
(→‎Solution 2)
 
Line 10: Line 10:
 
==Solution 2==
 
==Solution 2==
 
Notice that the equation is satisfied twice for every sine period (which is <math>\frac{2}{5}</math>), except in the sole case when the two equations equate to <math>0</math>. In that case, the equation is satisfied twice but only at the one instance when <math>y=0</math>. Hence, it is double-counted in our final solution, so we have to subtract it out. We then compute:
 
Notice that the equation is satisfied twice for every sine period (which is <math>\frac{2}{5}</math>), except in the sole case when the two equations equate to <math>0</math>. In that case, the equation is satisfied twice but only at the one instance when <math>y=0</math>. Hence, it is double-counted in our final solution, so we have to subtract it out. We then compute:
−
<math>32 * \frac{5}{2} * 2 - 1 = \boxed {159}</math>
+
<math>32 \cdot \frac{5}{2} \cdot 2 - 1 = \boxed {159}</math>
  
 
== See also ==
 
== See also ==

Latest revision as of 15:01, 26 November 2019

Problem

How many real numbers $x^{}_{}$ satisfy the equation $\frac{1}{5}\log_2 x = \sin (5\pi x)$?

Solution

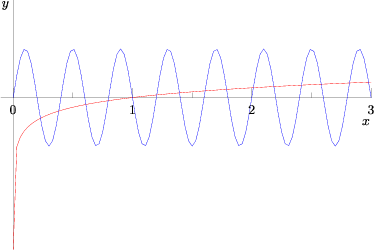
AIME 1991 Solution 04.png

The range of the sine function is $-1 \le y \le 1$. It is periodic (in this problem) with a period of $\frac{2}{5}$.

Thus, $-1 \le \frac{1}{5} \log_2 x \le 1$, and $-5 \le \log_2 x \le 5$. The solutions for $x$ occur in the domain of $\frac{1}{32} \le x \le 32$. When $x > 1$ the logarithm function returns a positive value; up to $x = 32$ it will pass through the sine curve. There are exactly 10 intersections of five periods (every two integral values of $x$) of the sine curve and another curve that is $< 1$, so there are $\frac{32}{2} \cdot 10 - 6 = 160 - 6 = 154$ values (the subtraction of 6 since all the “intersections” when $x < 1$ must be disregarded). When $y = 0$, there is exactly $1$ touching point between the two functions: $\left(\frac{1}{5},0\right)$. When $y < 0$ or $x < 1$, we can count $4$ more solutions. The solution is $154 + 1 + 4 = \boxed{159}$.

Solution 2

Notice that the equation is satisfied twice for every sine period (which is $\frac{2}{5}$), except in the sole case when the two equations equate to $0$. In that case, the equation is satisfied twice but only at the one instance when $y=0$. Hence, it is double-counted in our final solution, so we have to subtract it out. We then compute: $32 \cdot \frac{5}{2} \cdot 2 - 1 = \boxed {159}$

See also

1991 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 3 		Followed by
Problem 5
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1991_AIME_Problems/Problem_4&oldid=112207"