Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2020 AIME I Problems/Problem 1"

(→‎Animation and Video solution)
(→‎Solution 2)
 
(19 intermediate revisions by 12 users not shown)
Line 1: Line 1:
  
 
== Problem ==
 
== Problem ==
−
In <math>\triangle ABC</math> with <math>AB=AC,</math> point <math>D</math> lies strictly between <math>A</math> and <math>C</math> on side <math>\overline{AC},</math> and point <math>E</math> lies strictly between <math>A</math> and <math>B</math> on side <math>\overline{AB}</math> such that <math>AE=ED=DB=BC.</math> The degree measure of <math>\angle ABC</math> is <math>\tfrac{m}{n},</math> where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n.</math>
+
In <math>\triangle ABC</math> with <math>AB=AC,</math> point <math>D</math> lies strictly between <math>A</math> and <math>C</math> on side <math>\overline{AC},</math> and point <math>E</math> lies strictly between <math>A</math> and <math>B</math> on side <math>\overline{AB}</math> such that <math>AE=ED=DB=BC.</math> The degree measure of <math>\angle ABC</math> is <math>\tfrac{m}{n},</math> where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n.</math>  
  
 
== Solution 1==
 
== Solution 1==
Line 38: Line 38:
 
This tells us <math>\angle{BCA}=\angle{ABC}=3x</math> and <math>3x+3x+x=180</math>.
 
This tells us <math>\angle{BCA}=\angle{ABC}=3x</math> and <math>3x+3x+x=180</math>.
 
Thus <math>x=\frac{180}{7}</math> and we want <math>\angle{ABC}=3x=\frac{540}{7}</math> to get an answer of <math>\boxed{547}</math>.
 
Thus <math>x=\frac{180}{7}</math> and we want <math>\angle{ABC}=3x=\frac{540}{7}</math> to get an answer of <math>\boxed{547}</math>.
−
==Solution 3 (Official MAA)==
+
==Solution 3 (Official MAA)==  
 
Let <math>x = \angle ABC = \angle ACB</math>. Because <math>\triangle BCD</math> is isosceles, <math>\angle CBD = 180^\circ - 2x</math>. Then
 
Let <math>x = \angle ABC = \angle ACB</math>. Because <math>\triangle BCD</math> is isosceles, <math>\angle CBD = 180^\circ - 2x</math>. Then
 
<cmath>\angle DBE = x - \angle CBD = x - (180^\circ - 2x) =  3x - 180^\circ\!.</cmath>Because <math>\triangle EDA</math> and <math>\triangle DBE</math> are also isosceles,
 
<cmath>\angle DBE = x - \angle CBD = x - (180^\circ - 2x) =  3x - 180^\circ\!.</cmath>Because <math>\triangle EDA</math> and <math>\triangle DBE</math> are also isosceles,
Line 74: Line 74:
  
 
https://youtu.be/4XkA0DwuqYk
 
https://youtu.be/4XkA0DwuqYk
 +
 +
==Solution 4 (writing equations)==
 +
graph soon
 +
 +
We write equations based on the triangle sum of angles theorem. There are angles that do not need variables as the less variables the better.
 +
 +
<cmath>\begin{align*}
 +
\angle A &= y \\
 +
\angle B &= x+z \\
 +
\angle C &= \frac{180-x}{2} \\
 +
\end{align*}</cmath>
 +
 +
Then, using triangle sum of angles theorem, we find that
 +
 +
<cmath>\begin{align*}
 +
\angle A + \angle B + \angle C = x+y+z+\frac{180-x}{2}=180 \\
 +
\end{align*}</cmath>
 +
 +
Now we just need to find the variables.
 +
 +
<cmath>\begin{align*}
 +
(180-2y)+z = 180& \\
 +
(180-2z)+y+\frac{180-x}{2} = 180& \\
 +
\end{align*}</cmath>
 +
 +
Notice how all the equations equal 180. We can use this to write
 +
 +
<cmath>\begin{align*}
 +
(180-2y)+z = (180-2z)+y+\frac{180-x}{2}=x+y+z+\frac{180-x}{2} \\
 +
\end{align*}</cmath>
 +
 +
Simplifying, we get
 +
 +
<cmath>\begin{align*}
 +
(180-2y)+z=(180-2z)+y+\frac{180-x}{2} \\
 +
360-4y+2z=360-4z+2y+180-x \\
 +
\end{align*}</cmath>
 +
 +
<cmath>\begin{align*}
 +
6z=6y+180-x \\
 +
x=6y-6z+180 \\
 +
\end{align*}</cmath>
 +
 +
<cmath>\begin{align*}
 +
(180-2y)+z=6y-6z+180+y+z+\frac{180-(6y-6+180)}{2} \\
 +
360-4y+2z=12y-12z+360+2y+2z+180-6y+6z-180 \\
 +
\end{align*}</cmath>
 +
 +
<cmath>\begin{align*}
 +
6z=12y& \\
 +
z=2y& \\
 +
\end{align*}</cmath>
 +
 +
Theres more. We are at a dead end right now because we forgot that the problem states that the triangle is isosceles. With this, we can write the equation
 +
 +
<cmath>\begin{align*}
 +
\frac{180-x}{2}=x+z \\
 +
\end{align*}</cmath>
 +
 +
Substituting <math>z</math> with <math>2y</math>, we get
 +
 +
<cmath>\begin{align*}
 +
\frac{180-x}{2}=x+2y \\
 +
180-x=2x+4y \\
 +
\end{align*}</cmath>
 +
<cmath>\begin{align*}
 +
180-(6y-6z+180)=2(6y-6z+180)+4y& \\
 +
180-6y+12y-180=12y-24y+360+4y& \\
 +
\end{align*}</cmath>
 +
<cmath>\begin{align*}
 +
6y=-8y+360& \\
 +
\end{align*}</cmath>
 +
 +
With this, we get
 +
 +
<cmath>\begin{align*}
 +
y=\frac{180}{7} \\
 +
x=\frac{180}{7} \\
 +
z=\frac{360}{7} \\
 +
\end{align*}</cmath>
 +
 +
And a final answer of <math>\frac{180}{7}+\frac{360}{7} = \frac{540}{7} = \boxed{547}</math>.
 +
 +
~[[OrenSH|orenbad]]
 +
 +
== Video Solution by OmegaLearn ==
 +
https://youtu.be/O_o_-yjGrOU?t=333
 +
 +
~ pi_is_3.14
  
 
==Video solution==
 
==Video solution==
  
 
https://youtu.be/IH7yM3L5xjA
 
https://youtu.be/IH7yM3L5xjA
 +
 +
https://youtu.be/mgRNqSDCvgM ~yofro
 +
 +
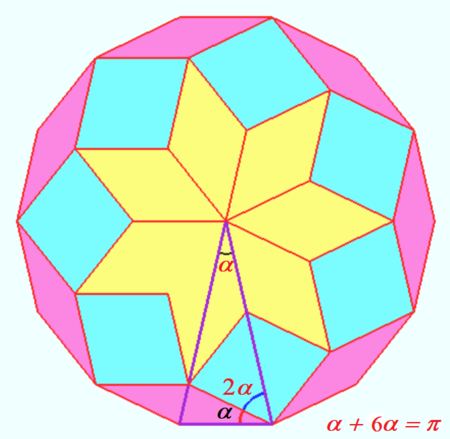
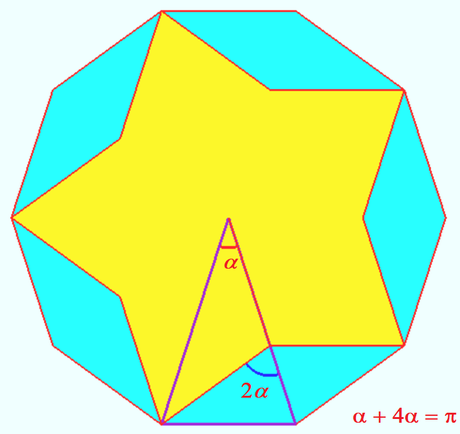
==Solution without words==
 +
[[File:2020 AIME I 1.png|450px|left]]
 +
[[File:2020 AIME I 1a.png|460px|right]]
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
  
 
==See Also==
 
==See Also==

Latest revision as of 14:01, 24 January 2024

Problem

In $\triangle ABC$ with $AB=AC,$ point $D$ lies strictly between $A$ and $C$ on side $\overline{AC},$ and point $E$ lies strictly between $A$ and $B$ on side $\overline{AB}$ such that $AE=ED=DB=BC.$ The degree measure of $\angle ABC$ is $\tfrac{m}{n},$ where $m$ and $n$ are relatively prime positive integers. Find $m+n.$

Solution 1

[asy] size(10cm); pair A, B, C, D, F; A = (0, tan(3 * pi / 7)); B = (1, 0); C = (-1, 0); F = rotate(90/7, A) * (A - (0, 2)); D = rotate(900/7, F) * A; draw(A -- B -- C -- cycle); draw(F -- D); draw(D -- B); label("$A$", A, N); label("$B$", B, E); label("$C$", C, W); label("$D$", D, W); label("$E$", F, E); [/asy]

If we set $\angle{BAC}$ to $x$, we can find all other angles through these two properties: 1. Angles in a triangle sum to $180^{\circ}$. 2. The base angles of an isosceles triangle are congruent.

Now we angle chase. $\angle{ADE}=\angle{EAD}=x$, $\angle{AED} = 180-2x$, $\angle{BED}=\angle{EBD}=2x$, $\angle{EDB} = 180-4x$, $\angle{BDC} = \angle{BCD} = 3x$, $\angle{CBD} = 180-6x$. Since $AB = AC$ as given by the problem, $\angle{ABC} = \angle{ACB}$, so $180-4x=3x$. Therefore, $x = 180/7^{\circ}$, and our desired angle is \[180-4\left(\frac{180}{7}\right) = \frac{540}{7}\] for an answer of $\boxed{547}$.

See here for a video solution: https://youtu.be/4e8Hk04Ax_E

Solution 2

Let $\angle{BAC}$ be $x$ in degrees. $\angle{ADE}=x$. By Exterior Angle Theorem on triangle $AED$, $\angle{BED}=2x$. By Exterior Angle Theorem on triangle $ADB$, $\angle{BDC}=3x$. This tells us $\angle{BCA}=\angle{ABC}=3x$ and $3x+3x+x=180$. Thus $x=\frac{180}{7}$ and we want $\angle{ABC}=3x=\frac{540}{7}$ to get an answer of $\boxed{547}$.

Solution 3 (Official MAA)

Let $x = \angle ABC = \angle ACB$. Because $\triangle BCD$ is isosceles, $\angle CBD = 180^\circ - 2x$. Then \[\angle DBE = x - \angle CBD = x - (180^\circ - 2x) = 3x - 180^\circ\!.\]Because $\triangle EDA$ and $\triangle DBE$ are also isosceles, \[\angle BAC =\frac12(\angle EAD + \angle ADE) = \frac12(\angle BED)= \frac12(\angle DBE)\] \[= \frac12 (3x - 180^\circ) = \frac32x-90^\circ\!.\] Because $\triangle ABC$ is isosceles, $\angle BAC$ is also $180^\circ-2x$, so $\frac32x - 90^\circ = 180^\circ - 2x$, and it follows that $\angle ABC = x = \left(\frac{540}7\right)^\circ$. The requested sum is $540+7 = 547$.

[asy] unitsize(4 cm); pair A, B, C, D, E; real a = 180/7; A = (0,0); B = dir(180 - a/2); C = dir(180 + a/2); D = extension(B, B + dir(270 + a), A, C); E = extension(D, D + dir(90 - 2*a), A, B); draw(A--B--C--cycle); draw(B--D--E); label("$A$", A, dir(0)); label("$B$", B, NW); label("$C$", C, SW); label("$D$", D, S); label("$E$", E, N); [/asy]

https://artofproblemsolving.com/wiki/index.php/1961_AHSME_Problems/Problem_25 (Almost Mirrored)

See here for a video solution:

https://youtu.be/4XkA0DwuqYk

Solution 4 (writing equations)

graph soon

We write equations based on the triangle sum of angles theorem. There are angles that do not need variables as the less variables the better.

\begin{align*} \angle A &= y \\ \angle B &= x+z \\ \angle C &= \frac{180-x}{2} \\ \end{align*}

Then, using triangle sum of angles theorem, we find that

\begin{align*} \angle A + \angle B + \angle C = x+y+z+\frac{180-x}{2}=180 \\ \end{align*}

Now we just need to find the variables.

\begin{align*} (180-2y)+z = 180& \\ (180-2z)+y+\frac{180-x}{2} = 180& \\ \end{align*}

Notice how all the equations equal 180. We can use this to write

\begin{align*} (180-2y)+z = (180-2z)+y+\frac{180-x}{2}=x+y+z+\frac{180-x}{2} \\ \end{align*}

Simplifying, we get

\begin{align*} (180-2y)+z=(180-2z)+y+\frac{180-x}{2} \\ 360-4y+2z=360-4z+2y+180-x \\ \end{align*}

\begin{align*} 6z=6y+180-x \\ x=6y-6z+180 \\ \end{align*}

\begin{align*} (180-2y)+z=6y-6z+180+y+z+\frac{180-(6y-6+180)}{2} \\ 360-4y+2z=12y-12z+360+2y+2z+180-6y+6z-180 \\ \end{align*}

\begin{align*} 6z=12y& \\ z=2y& \\ \end{align*}

Theres more. We are at a dead end right now because we forgot that the problem states that the triangle is isosceles. With this, we can write the equation

\begin{align*} \frac{180-x}{2}=x+z \\ \end{align*}

Substituting $z$ with $2y$, we get

\begin{align*} \frac{180-x}{2}=x+2y \\ 180-x=2x+4y \\ \end{align*} \begin{align*} 180-(6y-6z+180)=2(6y-6z+180)+4y& \\ 180-6y+12y-180=12y-24y+360+4y& \\ \end{align*} \begin{align*} 6y=-8y+360& \\ \end{align*}

With this, we get

\begin{align*} y=\frac{180}{7} \\ x=\frac{180}{7} \\ z=\frac{360}{7} \\ \end{align*}

And a final answer of $\frac{180}{7}+\frac{360}{7} = \frac{540}{7} = \boxed{547}$.

~orenbad

Video Solution by OmegaLearn

https://youtu.be/O_o_-yjGrOU?t=333

~ pi_is_3.14

Video solution

https://youtu.be/IH7yM3L5xjA

https://youtu.be/mgRNqSDCvgM ~yofro

Solution without words

2020 AIME I 1.png
2020 AIME I 1a.png

vladimir.shelomovskii@gmail.com, vvsss

See Also

2020 AIME I (Problems • Answer Key • Resources)
Preceded by
First Problem 		Followed by
Problem 2
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2020_AIME_I_Problems/Problem_1&oldid=212608"