Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2007 Cyprus MO/Lyceum/Problem 6"

(img)
 
Line 2: Line 2:
 
[[Image:2007 CyMO-6.PNG|250px]]
 
[[Image:2007 CyMO-6.PNG|250px]]
 
</div>
 
</div>
−
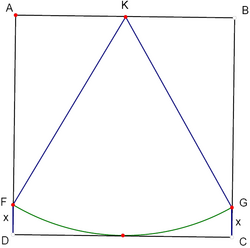
<math>\displaystyle ABCD</math> is a [[square]] of side length 2 and <math>FG</math> is an [[arc]] of the [[circle]] with centre the [[midpoint]] <math>K</math> of the side <math>\overline{AB}</math> and [[radius]] 2. The length of the segments <math>\displaystyle FD=GC=x</math> is
+
<math>\displaystyle ABCD</math> is a [[square]] of side length 2 and <math>FG</math> is an [[arc]] of the [[circle]] with centre the [[midpoint]] <math>K</math> of the side <math>AB</math> and [[radius]] 2. The length of the segments <math>\displaystyle FD=GC=x</math> is
  
 
<math> \mathrm{(A) \ } \frac 14\qquad \mathrm{(B) \ } \frac{\sqrt{2}}2\qquad \mathrm{(C) \ } 2-\sqrt{3}\qquad \mathrm{(D) \ } \sqrt{3} - 1\qquad \mathrm{(E) \ } \sqrt{2} - 1</math>
 
<math> \mathrm{(A) \ } \frac 14\qquad \mathrm{(B) \ } \frac{\sqrt{2}}2\qquad \mathrm{(C) \ } 2-\sqrt{3}\qquad \mathrm{(D) \ } \sqrt{3} - 1\qquad \mathrm{(E) \ } \sqrt{2} - 1</math>

Latest revision as of 09:39, 8 May 2007

2007 CyMO-6.PNG

$\displaystyle ABCD$ is a square of side length 2 and $FG$ is an arc of the circle with centre the midpoint $K$ of the side $AB$ and radius 2. The length of the segments $\displaystyle FD=GC=x$ is

$\mathrm{(A) \ } \frac 14\qquad \mathrm{(B) \ } \frac{\sqrt{2}}2\qquad \mathrm{(C) \ } 2-\sqrt{3}\qquad \mathrm{(D) \ } \sqrt{3} - 1\qquad \mathrm{(E) \ } \sqrt{2} - 1$

Solution

($F,\ G$ are on $\overline{AD},\ \overline{ BC}$, respectively)

Draw radii $\overline{KF},\ \overline{KG}$, both with length $2$. $\displaystyle AK = BK = 1$, so we form $30-60-90$ right triangles. $AF = BG = \sqrt{3}$, and so $DF = CG = 2 - \sqrt{3} \Longrightarrow \mathrm{C}$.

See also

2007 Cyprus MO, Lyceum (Problems)
Preceded by
Problem 5 		Followed by
Problem 7
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2007_Cyprus_MO/Lyceum/Problem_6&oldid=15045"