Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1995 AIME Problems/Problem 1"

 
 
(7 intermediate revisions by 3 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
 +
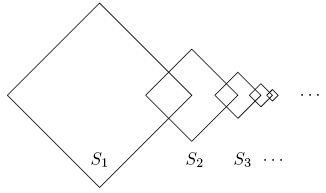
Square <math>S_{1}</math> is <math>1\times 1.</math>  For <math>i\ge 1,</math> the lengths of the sides of square <math>S_{i+1}</math> are half the lengths of the sides of square <math>S_{i},</math> two adjacent sides of square <math>S_{i}</math> are perpendicular bisectors of two adjacent sides of square <math>S_{i+1},</math> and the other two sides of square <math>S_{i+1},</math> are the perpendicular bisectors of two adjacent sides of square <math>S_{i+2}.</math>  The total area enclosed by at least one of <math>S_{1}, S_{2}, S_{3}, S_{4}, S_{5}</math> can be written in the form <math>m/n,</math> where <math>m</math> and <math>n</math> are relatively prime positive integers.  Find <math>m-n.</math>
  
 +
[[Image:AIME 1995 Problem 1.png]]
 
== Solution ==
 
== Solution ==
 +
The sum of the areas of the [[square]]s if they were not interconnected is a [[geometric sequence]]:
 +
 +
:<math>1^2 + \left(\frac{1}{2}\right)^2 + \left(\frac{1}{4}\right)^2 + \left(\frac{1}{8}\right)^2 + \left(\frac{1}{16}\right)^2</math>
 +
 +
Then subtract the areas of the intersections, which is <math>\left(\frac{1}{4}\right)^2 + \ldots + \left(\frac{1}{32}\right)^2</math>:
 +
 +
:<math>1^2 + \left(\frac{1}{2}\right)^2 + \left(\frac{1}{4}\right)^2 + \left(\frac{1}{8}\right)^2 + \left(\frac{1}{16}\right)^2 - \left[\left(\frac{1}{4}\right)^2 + \left(\frac{1}{8}\right)^2 + \left(\frac{1}{16}\right)^2 + \left(\frac{1}{32}\right)^2\right]</math>
 +
:<math>= 1 + \frac{1}{2}^2 - \frac{1}{32}^2</math>
 +
 +
The majority of the terms cancel, leaving <math>1 + \frac{1}{4} - \frac{1}{1024}</math>, which simplifies down to <math>\frac{1024 + \left(256 - 1\right)}{1024}</math>. Thus, <math>m-n =  \boxed{255}</math>.
 +
 +
Alternatively, take the area of the first square and add <math>\,\frac{3}{4}</math> of the areas of  the remaining squares. This results in <math>1+ \frac{3}{4}\left[\left(\frac{1}{2}\right)^2 + \ldots + \left(\frac{1}{16}^2\right)\right]</math>, which when simplified will produce the same answer.
  
 
== See also ==
 
== See also ==
−
* [[1995 AIME Problems]]
+
{{AIME box|year=1995|before=First Question|num-a=2}}
 +
 
 +
[[Category:Introductory Geometry Problems]]
 +
{{MAA Notice}}

Latest revision as of 18:29, 4 July 2013

Problem

Square $S_{1}$ is $1\times 1.$ For $i\ge 1,$ the lengths of the sides of square $S_{i+1}$ are half the lengths of the sides of square $S_{i},$ two adjacent sides of square $S_{i}$ are perpendicular bisectors of two adjacent sides of square $S_{i+1},$ and the other two sides of square $S_{i+1},$ are the perpendicular bisectors of two adjacent sides of square $S_{i+2}.$ The total area enclosed by at least one of $S_{1}, S_{2}, S_{3}, S_{4}, S_{5}$ can be written in the form $m/n,$ where $m$ and $n$ are relatively prime positive integers. Find $m-n.$

AIME 1995 Problem 1.png

Solution

The sum of the areas of the squares if they were not interconnected is a geometric sequence:

$1^2 + \left(\frac{1}{2}\right)^2 + \left(\frac{1}{4}\right)^2 + \left(\frac{1}{8}\right)^2 + \left(\frac{1}{16}\right)^2$

Then subtract the areas of the intersections, which is $\left(\frac{1}{4}\right)^2 + \ldots + \left(\frac{1}{32}\right)^2$:

$1^2 + \left(\frac{1}{2}\right)^2 + \left(\frac{1}{4}\right)^2 + \left(\frac{1}{8}\right)^2 + \left(\frac{1}{16}\right)^2 - \left[\left(\frac{1}{4}\right)^2 + \left(\frac{1}{8}\right)^2 + \left(\frac{1}{16}\right)^2 + \left(\frac{1}{32}\right)^2\right]$
$= 1 + \frac{1}{2}^2 - \frac{1}{32}^2$

The majority of the terms cancel, leaving $1 + \frac{1}{4} - \frac{1}{1024}$, which simplifies down to $\frac{1024 + \left(256 - 1\right)}{1024}$. Thus, $m-n = \boxed{255}$.

Alternatively, take the area of the first square and add $\,\frac{3}{4}$ of the areas of the remaining squares. This results in $1+ \frac{3}{4}\left[\left(\frac{1}{2}\right)^2 + \ldots + \left(\frac{1}{16}^2\right)\right]$, which when simplified will produce the same answer.

See also

1995 AIME (Problems • Answer Key • Resources)
Preceded by
First Question 		Followed by
Problem 2
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1995_AIME_Problems/Problem_1&oldid=55026"