Difference between revisions of "1995 AIME Problems/Problem 1"
(solution, box) |
(fix) |
||
| Line 4: | Line 4: | ||
[[Image:AIME 1995 Problem 1.png]] | [[Image:AIME 1995 Problem 1.png]] | ||
== Solution == | == Solution == | ||
| − | The sum of the areas of the [[square]]s if they were not interconnected is a [[geometric sequence]]: | + | The sum of the areas of the [[square]]s if they were not interconnected is a [[geometric sequence]]: |
| − | Alternatively, take the area of the first square and add <math>\frac{3}{4}</math> of the areas of the remaining squares. This results in <math>1 + \frac{3}{4}(\frac{1}{2}^2 + \ | + | :<math>1^2 + (\frac{1}{2})^2 + (\frac{1}{4})^2 + (\frac{1}{8})^2 + (\frac{1}{16})^2</math> |
| + | |||
| + | Then subtract the areas of the intersections (<math>(\frac{1}{4})^2 + \ldots + (\frac{1}{32})^2</math>): | ||
| + | |||
| + | :<math>1^2 + (\frac{1}{2})^2 + (\frac{1}{4})^2 + (\frac{1}{8})^2 + (\frac{1}{16})^2 - [(\frac{1}{4})^2 + (\frac{1}{8})^2 + (\frac{1}{16})^2 + (\frac{1}{32})^2]</math> | ||
| + | :<math>= 1 + \frac{1}{2}^2 - \frac{1}{32}^2</math> | ||
| + | |||
| + | The majority of the terms cancel, leaving <math>1 + \frac{1}{4} - \frac{1}{1024}</math>, which simplifies down to <math>\frac{1024 + (256 - 1)}{1024}</math>. Thus, <math>m-n = 255</math>. | ||
| + | |||
| + | Alternatively, take the area of the first square and add <math>\,\frac{3}{4}</math> of the areas of the remaining squares. This results in <math>1+ \frac{3}{4}(\frac{1}{2}^2 + \ldots + \frac{1}{16}^2)</math>, which when simplified will produce the same answer. | ||
== See also == | == See also == | ||
Revision as of 21:56, 8 February 2007
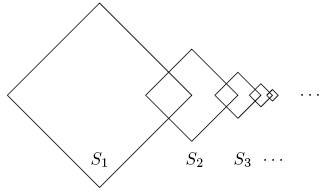
Problem
Square ![]() is
is ![]() For
For ![]() the lengths of the sides of square
the lengths of the sides of square ![]() are half the lengths of the sides of square
are half the lengths of the sides of square ![]() two adjacent sides of square
two adjacent sides of square ![]() are perpendicular bisectors of two adjacent sides of square
are perpendicular bisectors of two adjacent sides of square ![]() and the other two sides of square
and the other two sides of square ![]() are the perpendicular bisectors of two adjacent sides of square
are the perpendicular bisectors of two adjacent sides of square ![]() The total area enclosed by at least one of
The total area enclosed by at least one of ![]() can be written in the form
can be written in the form ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Solution
The sum of the areas of the squares if they were not interconnected is a geometric sequence:
Then subtract the areas of the intersections (![]() ):
):
The majority of the terms cancel, leaving ![]() , which simplifies down to
, which simplifies down to ![]() . Thus,
. Thus, ![]() .
.
Alternatively, take the area of the first square and add ![]() of the areas of the remaining squares. This results in
of the areas of the remaining squares. This results in ![]() , which when simplified will produce the same answer.
, which when simplified will produce the same answer.
See also
| 1995 AIME (Problems • Answer Key • Resources) | ||
| Preceded by First Question |
Followed by Problem 2 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||