Difference between revisions of "2007 Cyprus MO/Lyceum/Problem 21"
I_like_pie (talk | contribs) m |
m |
||
| Line 7: | Line 7: | ||
==Solution== | ==Solution== | ||
| − | The lengths of the straight parts of the strap are <math>3\,\mathrm{m}</math>, <math>4\,\mathrm{m}</math>, and <math>5\,\mathrm{m}</math>. Their sum is <math>12\,\mathrm{m}</math>. The curved parts of the band add up to a full circumference of one of the circles, so their sum is <math>20\pi\,\mathrm{ | + | The lengths of the straight parts of the strap are <math>3\,\mathrm{m}</math>, <math>4\,\mathrm{m}</math>, and <math>5\,\mathrm{m}</math>. Their sum is <math>12\,\mathrm{m}</math>. The curved parts of the band add up to a full circumference of one of the circles, so their sum is <math>20\pi\,\mathrm{ cm}</math>. The total length of the strap is <math>(12+\frac\pi5)\,\mathrm{m}\Longrightarrow\mathrm{D}</math>. |
==See also== | ==See also== | ||
{{CYMO box|year=2007|l=Lyceum|num-b=20|num-a=22}} | {{CYMO box|year=2007|l=Lyceum|num-b=20|num-a=22}} | ||
Latest revision as of 21:21, 23 July 2020
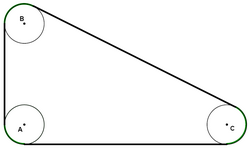
Problem
In the figure, three equal cycles of diameter 
represent pulleys, that are connected with a strap. If the distances between any two pulley center points are 
, 
and 
, then the length of the strap is
Solution
The lengths of the straight parts of the strap are 
, 
, and 
. Their sum is 
. The curved parts of the band add up to a full circumference of one of the circles, so their sum is 
. The total length of the strap is 
.
See also
| 2007 Cyprus MO, Lyceum (Problems) | ||
| Preceded by Problem 20 |
Followed by Problem 22 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
