Difference between revisions of "2007 AMC 12A Problems/Problem 10"
m (→Problem) |
(soln) |
||
| Line 1: | Line 1: | ||
| + | {{duplicate|[[2007 AMC 12A Problems|2007 AMC 12A #10]] and [[2007 AMC 10A Problems/Problem 14|2007 AMC 10A #14]]}} | ||
| + | |||
==Problem== | ==Problem== | ||
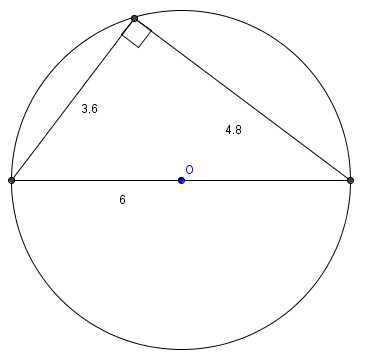
A [[triangle]] with side lengths in the [[ratio]] <math>3 : 4 : 5</math> is inscribed in a [[circle]] with [[radius]] 3. What is the area of the triangle? | A [[triangle]] with side lengths in the [[ratio]] <math>3 : 4 : 5</math> is inscribed in a [[circle]] with [[radius]] 3. What is the area of the triangle? | ||
| Line 11: | Line 13: | ||
==See also== | ==See also== | ||
{{AMC12 box|year=2007|ab=A|num-b=9|num-a=11}} | {{AMC12 box|year=2007|ab=A|num-b=9|num-a=11}} | ||
| + | {{AMC10 box|year=2007|ab=A|num-b=13|num-a=15}} | ||
[[Category:Introductory Geometry Problems]] | [[Category:Introductory Geometry Problems]] | ||
Revision as of 18:42, 5 January 2008
- The following problem is from both the 2007 AMC 12A #10 and 2007 AMC 10A #14, so both problems redirect to this page.
Problem
A triangle with side lengths in the ratio 
is inscribed in a circle with radius 3. What is the area of the triangle?
Solution
Since 3-4-5 is a Pythagorean triple, the triangle is a right triangle. Since the hypotenuse is a diameter of the circumcircle, the hypotenuse is 
. Then the other legs are 
and 
. The area is 
See also
| 2007 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 9 |
Followed by Problem 11 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
| 2007 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
