2024 AMC 10A Problems

2024 AMC 10A (Answer Key) Printable versions: Wiki • AoPS Resources • PDF
Instructions This is a 25-question, multiple choice test. Each question is followed by answers marked A, B, C, D and E. Only one of these is correct. You will receive 6 points for each correct answer, 2.5 points for each problem left unanswered if the year is before 2006, 1.5 points for each problem left unanswered if the year is after 2006, and 0 points for each incorrect answer. No aids are permitted other than scratch paper, graph paper, ruler, compass, protractor and erasers (and calculators that are accepted for use on the SAT if before 2006. No problems on the test will require the use of a calculator). Figures are not necessarily drawn to scale. You will have 75 minutes working time to complete the test.
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25

Problem 1

What is the value of $9901 \cdot 101 - 99 \cdot 10101$ ?

$\textbf{(A)}~2\qquad\textbf{(B)}~20\qquad\textbf{(C)}~200\qquad\textbf{(D)}~202\qquad\textbf{(E)}~2020$

Solution

Problem 2

Define $\blacktriangledown(a) = \sqrt{a - 1}$ and $\blacktriangle(a) = \sqrt{a + 1}$ for all real numbers $a$ . What is the value of $\frac{\blacktriangledown(20 + \blacktriangle(2024))}{\blacktriangledown(\blacktriangle(24))}~?$

$\textbf{(A)}~ 1 \qquad \textbf{(B)}~ 2 \qquad \textbf{(C)}~ 4 \qquad \textbf{(D)}~ 8 \qquad \textbf{(E)}~ 16$

Solution

Problem 3

What is the sum of the digits of the smallest prime that can be written as a sum of $5$ distinct primes?

$\textbf{(A)}~5\qquad\textbf{(B)}~7\qquad\textbf{(C)}~9\qquad\textbf{(D)}~10\qquad\textbf{(E)}~11$

Solution

Problem 4

A square and an isosceles triangle are joined along an edge to form a pentagon $10$ inches tall and $22$ inches wide, as shown below. What is the perimeter of the pentagon, in inches?

$[asy] import graph; size(7cm); real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ pen GGG = grey; draw((10, 0)--(0, 0)--(0, 10)--(10, 10)); draw((10, 0)--(10, 10), dashed); draw((10, 0)--(22, 5)--(10, 10)); draw((-1.5, 0)--(-1.5, 10), arrow = ArcArrow(SimpleHead), GGG); draw((-1.5, 10)--(-1.5, 0), arrow = ArcArrow(SimpleHead), GGG); draw((0, 11.5)--(22, 11.5), arrow = ArcArrow(SimpleHead), GGG); draw((22, 11.5)--(0, 11.5), arrow = ArcArrow(SimpleHead), GGG); label("$10$ in.", (-3.5, 5), GGG); label("$22$ in.", (11, 12.75), GGG); dot((0, 0)); dot((0, 10)); dot((10, 10)); dot((10, 0)); dot((22, 5)); [/asy]$

$\textbf{(A)}~54\qquad \textbf{(B)}~56 \qquad \textbf{(C)}~62 \qquad \textbf{(D)}~64 \qquad \textbf{(E)}~66$

Solution

Problem 5

Andrea is taking a series of several exams. If Andrea earns $61$ points on her next exam, her average score will decrease by $3$ points. If she instead earns $93$ points on her next exam, her average score will increase by $1$ point. How many points should Andrea earn on her next exam to keep her average score constant?

$\textbf{(A)}~80 \qquad\textbf{(B)}~82 \qquad\textbf{(C)}~83 \qquad\textbf{(D)}~85 \qquad\textbf{(E)}~86$

Solution

Problem 6

How many ordered pairs $(m, n)$ of positive integers exist such that $m$ is a factor of $54$ and $mn$ is a factor of $70$ ?

$\textbf{(A)}~2 \qquad\textbf{(B)}~4 \qquad\textbf{(C)}~10 \qquad\textbf{(D)}~12 \qquad\textbf{(E)}~16$

Solution

Problem 7

Let $M$ be the midpoint of segment $\overline{AB}$ , and let $T$ lie on segment $\overline{AB}$ so that $AT \cdot AM = 100$ and $BT \cdot BM = 28$ . What is the length of segment $\overline{TM}$ ?

$\textbf{(A)}~4\qquad \textbf{(B)}~4.5\qquad \textbf{(C)}~5 \qquad \textbf{(D)}~5.5 \qquad \textbf{(E)}~6$

Solution

Problem 8

In how many ways can $6$ juniors and $6$ seniors form $3$ disjoint teams of $4$ people so that each team has $2$ juniors and $2$ seniors?

$\textbf{(A)}~720\qquad\textbf{(B)}~1350\qquad\textbf{(C)}~2700\qquad\textbf{(D)}~3280\qquad\textbf{(E)}~8100$

Solution

Problem 9

Let $N$ be the least positive integer that is divisible by at least $3$ odd primes and at least $4$ perfect squares. What is the sum of the squares of the digits of $N$ ?

$\textbf{(A)}~ 41 \qquad \textbf{(B)}~ 65 \qquad \textbf{(C)}~ 80 \qquad \textbf{(D)}~ 89 \qquad \textbf{(E)}~ 100$

Solution

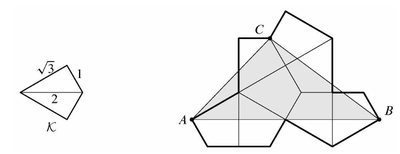
Problem 10

Let $\mathcal{K}$ be the kite formed by joining two right triangles with legs $1$ and $\sqrt{3}$ along a common hypotenuse. Eight copies of $\mathcal{K}$ are used to form the polygon shown below. What is the area of triangle $\triangle ABC$ ?

$\textbf{(A)}~2 + 3\sqrt{3} \qquad\textbf{(B)}~\frac{9\sqrt{3}}{2} \qquad\textbf{(C)}~\frac{10 + 8\sqrt{3}}{3} \qquad\textbf{(D)}~8 \qquad\textbf{(E)}~5\sqrt{3}$

Solution

Problem 11

If $x$ and $y$ are real numbers satisfying $x + \tfrac{x}{y} = 2$ and $y + \tfrac{y}{x} = 6$ , what is the value of $x + y$ ?

$\textbf{(A)}~\frac{101}{28} \qquad\textbf{(B)}~\frac{42}{11} \qquad\textbf{(C)}~\frac{30}{7} \qquad\textbf{(D)}~\frac{14}{3} \qquad\textbf{(E)}~\frac{110}{21}$

Solution

Problem 12

Square $ABCD$ has side length $6$ and center $O$ . Points $E$ and $F$ lie in the plane, and $AOEF$ is a rectangle. Suppose that exactly $\tfrac{2}{3}$ of the area of $AOEF$ lies inside square $ABCD$ . What is the area of $\triangle CEF$ ?

$\textbf{(A)}~4\qquad\textbf{(B)}~3\sqrt{2}\qquad\textbf{(C)}~6\qquad\textbf{(D)}~4\sqrt{3}\qquad\textbf{(E)}~8$

Solution

Problem 13

Aubrey raced his younger brother Blair. Aubrey runs at a faster constant speed than Blair, so Blair started the race $40$ feet ahead of Aubrey. Aubrey caught up to Blair after $8$ seconds, finishing the race $90$ feet ahead of Blair and $5$ seconds earlier than Blair. How far did Aubrey run, in feet?

$\textbf{(A)}~454\qquad\textbf{(B)}~494\qquad\textbf{(C)}~518\qquad\textbf{(D)}~558\qquad\textbf{(E)}~598$

Solution

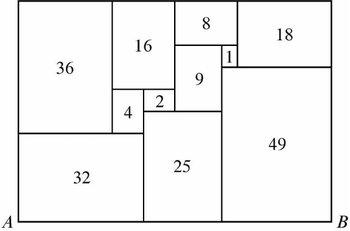
Problem 14

All of the rectangles in the figure below, which is drawn to scale, are similar to the enclosing rectangle. Each number represents the area of the rectangle. What is the length $AB$ ?

$\textbf{(A)}~4 + 4\sqrt{5}\qquad\textbf{(B)}~10\sqrt{2}\qquad\textbf{(C)}~5 + 5\sqrt{5}\qquad\textbf{(D)}~10\sqrt[4]{8}\qquad\textbf{(E)}~20$

Solution

Problem 15

Let $S$ be a subset of $\{1, 2, 3, \cdots, 2024\}$ such that the following two conditions hold:

If $x$ and $y$ are distinct elements of $S$ , then $|x - y| > 2$ .
If $x$ and $y$ are distinct odd elements of $S$ , then $|x - y| > 6$ .

What is the maximum possible number of elements in $S$ ?

$\textbf{(A)}~436\qquad\textbf{(B)}~506\qquad\textbf{(C)}~608\qquad\textbf{(D)}~654\qquad\textbf{(E)}~675$

Solution

Problem 16

In how many ways can the integers $1$ , $2$ , $3$ , $4$ , $5$ , and $6$ be arranged in a line so that the following statement is true? If $2$ is not adjacent to $3$ , then $3$ is not adjacent to $4$ .

$\textbf{(A)}~480 \qquad\textbf{(B)}~504 \qquad\textbf{(C)}~528 \qquad\textbf{(D)}~572 \qquad\textbf{(E)}~600$

Solution

Problem 17

The numbers, in order, of each row and the numbers, in order, of each column of a $5 \times 5$ array of integers form an arithmetic progression of length $5$ . The numbers in positions $(5, 5)$ , $(2, 4)$ , $(4, 3)$ , and $(3, 1)$ are $0$ , $48$ , $16$ , and $12$ , respectively. What number is in position $(1, 2)$ ? $\begin{bmatrix}. & ? & . & . & . \\. & . & . & 48 & . \\ 12 & . & . & . & . \\ . & . & 16 & . & . \\ . & . & . & . & 0\end{bmatrix}$

$\textbf{(A)}~19\qquad\textbf{(B)}~24\qquad\textbf{(C)}~29\qquad\textbf{(D)}~34\qquad\textbf{(E)}~39$

Solution

Problem 18

Points $X$ and $Y$ lie on sides $\overline{BC}$ and $\overline{CD}$ , respectively, of parallelogram $ABCD$ such that $\angle AXC = \angle AYC = 90^{\circ}$ . Suppose $BX = 5$ and $DY = 3$ , as shown. If $ABCD$ has perimeter $48$ , what is its area?

$[asy] import olympiad; import graph; size(8cm); real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ pair A = (0, 0), B = (15, 0), C = (12, -6 * sqrt(2)), D = (-3, -6 * sqrt(2)); pair X = (15 - 3 * 5/9, -6 * sqrt(2) * 5 / 9); pair Y = (0, -6 * sqrt(2)); dot(A); dot(B); dot(C); dot(D); dot(X); dot(Y); draw(A--B--C--D--cycle); draw(A--X); draw(A--Y); draw(rightanglemark(A,X,C,15)); draw(rightanglemark(A,Y,C,15)); label("$A$", A, N * 1.5); label("$B$", B, N * 1.5); label("$C$", C, S * 1.5); label("$D$", D, S * 1.5); label("$X$", X, E * 1.5); label("$Y$", Y, S * 1.5); label("$3$", midpoint(D--Y), S * 1.5); label("$5$", midpoint(B--X), E * 1.5); [/asy]$

$\textbf{(A)}~40\sqrt{5}\qquad\textbf{(B)}~56\sqrt{3}\qquad\textbf{(C)}~48\sqrt{7}\qquad\textbf{(D)}~90\sqrt{2}\qquad\textbf{(E)}~60\sqrt{5}$

Solution

Problem 19

A bee is moving in three-dimensional space. A fair six-sided die with faces labeled $A^{+}, A^{-}, B^{+}, B^{-}, C^{+}$ , and $C^{-}$ is rolled. Suppose the bee occupies the point $(a, b, c)$ . If the die shows $A^{+}$ , then the bee moves to the point $(a + 1, b, c)$ and if the die shows $A^{-}$ , then the bee moves to the point $(a - 1, b, c)$ . Analogous moves are made with the other four outcomes. Suppose the bee starts at the point $(0, 0, 0)$ and the die is rolled four times. What is the probability that the bee traverses four distinct edges of some unit cube?

$\textbf{(A)}~\frac{1}{54}\qquad\textbf{(B)}~\frac{7}{54}\qquad\textbf{(C)}~\frac{1}{6}\qquad\textbf{(D)}~\frac{5}{18}\qquad\textbf{(E)}~\frac{2}{5}$

Solution

Problem 20

Point $X$ lies outside regular pentagon $ABCDE$ so that $\triangle BXE$ is an equilateral triangle, as shown below. What is the degree measure of acute angle $\angle CXD$ ?

$[asy] import graph; size(7cm); real labelscalefactor = 0.75; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ real xmin = -1.089556028373145, xmax = 2.738320502950249, ymin = -1.3143096399343266, ymax = 1.2691431521185288; /* image dimensions */ pen qqwuqq = rgb(0,0.39215686274509803,0); filldraw(arc((1.9562952014676112,0),0.25,168,192)--(1.9562952014676112,0)--cycle, mediumgrey); /* draw figures */ draw((-0.8090169943749473,0.5877852522924731)--(0.30901699437494745,0.9510565162951535)); draw((0.30901699437494745,0.9510565162951535)--(1,0)); draw((1,0)--(0.3090169943749473,-0.9510565162951536)); draw((0.3090169943749473,-0.9510565162951536)--(-0.8090169943749475,-0.587785252292473)); draw((-0.8090169943749475,-0.587785252292473)--(-0.8090169943749473,0.5877852522924731)); draw((0.30901699437494745,0.9510565162951535)--(0.3090169943749473,-0.9510565162951536)); draw((0.3090169943749473,-0.9510565162951536)--(1.9562952014676112,0)); draw((1.9562952014676112,0)--(0.30901699437494745,0.9510565162951535)); draw((-0.8090169943749473,0.5877852522924731)--(1.9562952014676112,0), dashed); draw((1.9562952014676112,0)--(-0.8090169943749475,-0.587785252292473), dashed); /* dots and labels */ dot((1,0),linewidth(4pt) + dotstyle); label("$A$", (1.013592864312142,0), E * labelscalefactor); dot((0.30901699437494745,0.9510565162951535),linewidth(4pt) + dotstyle); label("$B$", (0.26,1), NE * labelscalefactor); dot((-0.8090169943749473,0.5877852522924731),linewidth(4pt) + dotstyle); label("$C$", (-0.82,0.64), NW * 0.25); dot((-0.8090169943749475,-0.587785252292473),linewidth(4pt) + dotstyle); label("$D$", (-0.82,-0.64), SW * 0.25); dot((0.3090169943749473,-0.9510565162951536),linewidth(4pt) + dotstyle); label("$E$", (0.26,-1), SE * labelscalefactor); dot((1.9562952014676112,0),linewidth(4pt) + dotstyle); label("$X$", (1.9705619971429902, 0), E * labelscalefactor); clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); /* end of picture */ [/asy]$

$\textbf{(A)}~18^{\circ}\qquad\textbf{(B)}~19.5^{\circ}\qquad\textbf{(C)}~21^{\circ}\qquad\textbf{(D)}~22.5^{\circ}\qquad\textbf{(E)}~24^{\circ}$

Solution

Problem 21

A fair six-sided die is repeatedly rolled until the same number is rolled twice in a row. What is the probability that the last number rolled is equal to the first number rolled?

$\textbf{(A)}~\frac{17}{72} \qquad\textbf{(B)}~\frac{4}{15} \qquad\textbf{(C)}~\frac{5}{18} \qquad\textbf{(D)}~\frac{2}{7} \qquad\textbf{(E)}~\frac{3}{10}$

Solution

Problem 22

Let $a$ , $b$ , and $c$ be pairwise relatively prime positive integers. Suppose one of these numbers is prime, and the other two are perfect squares. If $abc$ has $15a$ divisors and $a^{2}b^{2}c^{2}$ has $15b$ divisors, what is the least possible value of $a + b + c$ ?

$\textbf{(A)}~18\qquad\textbf{(B)}~44\qquad\textbf{(C)}~108\qquad\textbf{(D)}~141\qquad\textbf{(E)}~636$

Solution

Problem 23

The figure below shows a dotted grid $8$ cells wide and $3$ cells tall consisting of $1^{\prime\prime} \times 1^{\prime\prime}$ squares. Carl places $1$ -inch toothpicks along some of the sides of the squares to create a closed loop that does not intersect itself. The numbers in the cells indicate the number of sides of that square that are to be covered by toothpicks, and any number of toothpicks are allowed if no number is written. In how many ways can Carl place the toothpicks?

$[asy] size(6cm); for (int i=0; i<9; ++i) { draw((i,0)--(i,3),dotted); } for (int i=0; i<4; ++i){ draw((0,i)--(8,i),dotted); } for (int i=0; i<8; ++i) { for (int j=0; j<3; ++j) { if (j==1) { label("1",(i+0.5,1.5)); }}} [/asy]$

$\textbf{(A)}~130\qquad\textbf{(B)}~144\qquad\textbf{(C)}~146\qquad\textbf{(D)}~162\qquad\textbf{(E)}~196$

Solution

Problem 24

There exists a unique two-digit prime number $p$ such that both $4^{28} - 15$ and $3^{28} - 20$ are divisible by $p$ . What is the sum of the digits of $p$ ?

$\textbf{(A)}~10\qquad\textbf{(B)}~11\qquad\textbf{(C)}~13\qquad\textbf{(D)}~14\qquad\textbf{(E)}~16$

Solution

Problem 25

In parallelogram $ABCD$ , let $\omega$ be the circle with diameter $\overline{AD}$ and suppose $P$ and $Q$ are points on $\omega$ such that both lines $BP$ and $BQ$ are tangent to $\omega$ . If $BC = 8$ , $BP = 3$ , and line $PQ$ bisects $\overline{CD}$ , what is $AC^{2}$ ?

$\textbf{(A)}~180\qquad\textbf{(B)}~181\qquad\textbf{(C)}~182\qquad\textbf{(D)}~183\qquad\textbf{(E)}~184$

Solution

2024 AMC 10A (Problems • Answer Key • Resources)
Preceded by 2023 AMC 10B Problems	Followed by 2024 AMC 10B Problems
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

Page

Toolbox

Search

2024 AMC 10A Problems

Contents

Problem 1

Problem 2

Problem 3

Problem 4

Problem 5

Problem 6

Problem 7

Problem 8

Problem 9

Problem 10

Problem 11

Problem 12

Problem 13

Problem 14

Problem 15

Problem 16

Problem 17

Problem 18

Problem 19

Problem 20

Problem 21

Problem 22

Problem 23

Problem 24

Problem 25

See also