Difference between revisions of "1985 AIME Problems/Problem 9"
I_like_pie (talk | contribs) (→See also) |
m (imgs) |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
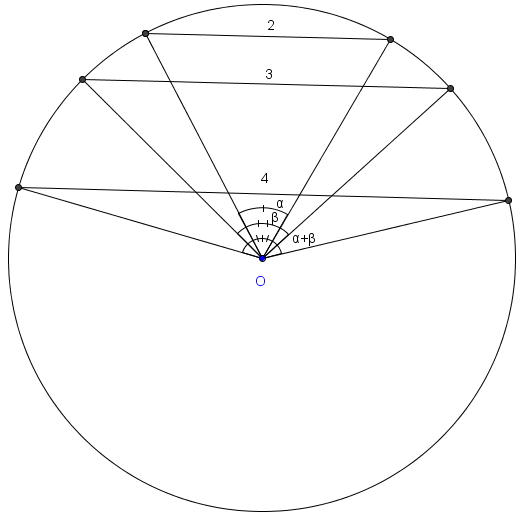
In a [[circle]], [[parallel]] [[chord]]s of [[length]]s 2, 3, and 4 determine [[central angle]]s of <math>\alpha</math>, <math>\beta</math>, and <math>\alpha + \beta</math> [[radian]]s, respectively, where <math>\alpha + \beta < \pi</math>. If <math>\cos \alpha</math>, which is a [[positive]] [[rational number]], is expressed as a [[fraction]] in lowest terms, what is the sum of its [[numerator]] and [[denominator]]? | In a [[circle]], [[parallel]] [[chord]]s of [[length]]s 2, 3, and 4 determine [[central angle]]s of <math>\alpha</math>, <math>\beta</math>, and <math>\alpha + \beta</math> [[radian]]s, respectively, where <math>\alpha + \beta < \pi</math>. If <math>\cos \alpha</math>, which is a [[positive]] [[rational number]], is expressed as a [[fraction]] in lowest terms, what is the sum of its [[numerator]] and [[denominator]]? | ||
| + | |||
== Solution == | == Solution == | ||
| + | [[Image:1985_AIME-9.png]] | ||
| + | |||
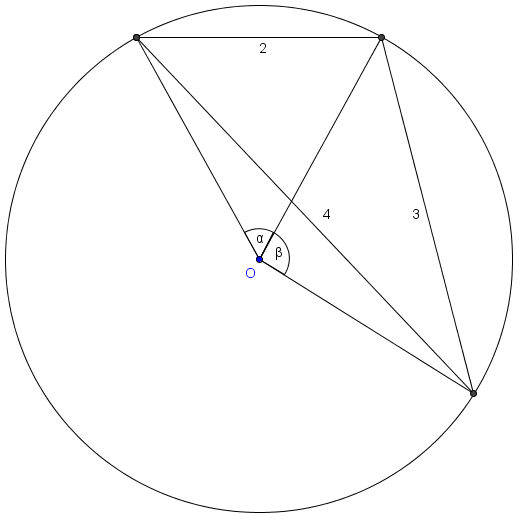
All chords of a given length in a given circle subtend the same [[arc]] and therefore the same central angle. Thus, by the given, we can re-arrange our chords into a [[triangle]] with the circle as its [[circumcircle]]. | All chords of a given length in a given circle subtend the same [[arc]] and therefore the same central angle. Thus, by the given, we can re-arrange our chords into a [[triangle]] with the circle as its [[circumcircle]]. | ||
| − | + | [[Image:1985_AIME-9a.png]] | |
This triangle has [[semiperimeter]] <math>\frac{2 + 3 + 4}{2}</math> so by [[Heron's formula]] it has [[area]] <math>K = \sqrt{\frac92 \cdot \frac52 \cdot \frac32 \cdot \frac12} = \frac{3}{4}\sqrt{15}</math>. The area of a given triangle with sides of length <math>a, b, c</math> and circumradius of length <math>R</math> is also given by the formula <math>K = \frac{abc}{4R}</math>, so <math>\frac6R = \frac{3}{4}\sqrt{15}</math> and <math>R = \frac8{\sqrt{15}}</math>. | This triangle has [[semiperimeter]] <math>\frac{2 + 3 + 4}{2}</math> so by [[Heron's formula]] it has [[area]] <math>K = \sqrt{\frac92 \cdot \frac52 \cdot \frac32 \cdot \frac12} = \frac{3}{4}\sqrt{15}</math>. The area of a given triangle with sides of length <math>a, b, c</math> and circumradius of length <math>R</math> is also given by the formula <math>K = \frac{abc}{4R}</math>, so <math>\frac6R = \frac{3}{4}\sqrt{15}</math> and <math>R = \frac8{\sqrt{15}}</math>. | ||
Revision as of 17:13, 11 September 2007
Problem
In a circle, parallel chords of lengths 2, 3, and 4 determine central angles of 
, 
, and 
radians, respectively, where 
. If 
, which is a positive rational number, is expressed as a fraction in lowest terms, what is the sum of its numerator and denominator?
Solution
All chords of a given length in a given circle subtend the same arc and therefore the same central angle. Thus, by the given, we can re-arrange our chords into a triangle with the circle as its circumcircle.
This triangle has semiperimeter 
so by Heron's formula it has area 
. The area of a given triangle with sides of length 
and circumradius of length 
is also given by the formula 
, so 
and 
.
Now, consider the triangle formed by two radii and the chord of length 2. This isosceles triangle has vertex angle , so by the Law of Cosines,
and so 
and the answer is 
.
See also
| 1985 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 8 |
Followed by Problem 10 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
