Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2007 Cyprus MO/Lyceum/Problem 22"

 
m (→‎Solution)
 
(4 intermediate revisions by 3 users not shown)
Line 2: Line 2:
 
[[Image:2007 CyMO-22.PNG|200px]]
 
[[Image:2007 CyMO-22.PNG|200px]]
  
−
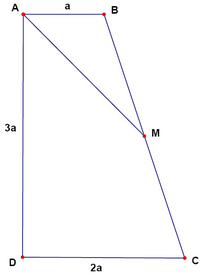
In the figure, <math>ABCD</math> is an orthogonal trapezium with <math>\ang A= \ang D=90^\circ</math> and bases <math>AB = a</math> , <math>DC = 2a</math> . If <math>AD = 3a</math> and <math>M</math> is the midpoint of the side <math>BC</math>, then <math>AM</math> equals to
+
In the figure, <math>ABCD</math> is an orthogonal trapezium with <math>\angle A= \angle D=90^\circ</math> and bases <math>AB = a</math> , <math>DC = 2a</math> . If <math>AD = 3a</math> and <math>M</math> is the midpoint of the side <math>BC</math>, then <math>AM</math> equals to
  
 
<math> \mathrm{(A) \ } \frac{3a}{2}\qquad \mathrm{(B) \ } \frac{3a}{\sqrt{2}}\qquad \mathrm{(C) \ } \frac{5a}{2}\qquad \mathrm{(D) \ } \frac{3a}{\sqrt{3}}\qquad \mathrm{(E) \ } 2a</math>
 
<math> \mathrm{(A) \ } \frac{3a}{2}\qquad \mathrm{(B) \ } \frac{3a}{\sqrt{2}}\qquad \mathrm{(C) \ } \frac{5a}{2}\qquad \mathrm{(D) \ } \frac{3a}{\sqrt{3}}\qquad \mathrm{(E) \ } 2a</math>
  
 
==Solution==
 
==Solution==
−
Let the midpoint of <math>AD</math> be <math>N</math>. The length of <math>MN</math> is the average of the bases, or <math>\frac{3a}{2}</math>. The length of <math>AN</math> is also <math>\frac{3a}{2}</math>. Since <math>\triangle AMN</math> is a 45-45-90 triangle, the length of <math>AM</math> is <math>\frac{3a}{\sqrt{2}}\Longrightarrow\mathrm{B}</math>
+
Let the midpoint of <math>AD</math> be <math>N</math>. The length of <math>MN</math> is the average of the bases, or <math>\frac{3a}{2}</math>. The length of <math>AN</math> is also <math>\frac{3a}{2}</math>.
 +
 
 +
Since <math>AMN</math> is a <math>45-45-90</math> triangle, the length of <math>AM</math> is <math>\frac{3a}{\sqrt{2}}</math>, and the answer is <math>\boxed{\mathrm{B}}</math>.
  
 
==See also==
 
==See also==
 
{{CYMO box|year=2007|l=Lyceum|num-b=21|num-a=23}}
 
{{CYMO box|year=2007|l=Lyceum|num-b=21|num-a=23}}

Latest revision as of 02:33, 19 January 2024

Problem

2007 CyMO-22.PNG

In the figure, $ABCD$ is an orthogonal trapezium with $\angle A= \angle D=90^\circ$ and bases $AB = a$ , $DC = 2a$ . If $AD = 3a$ and $M$ is the midpoint of the side $BC$, then $AM$ equals to

$\mathrm{(A) \ } \frac{3a}{2}\qquad \mathrm{(B) \ } \frac{3a}{\sqrt{2}}\qquad \mathrm{(C) \ } \frac{5a}{2}\qquad \mathrm{(D) \ } \frac{3a}{\sqrt{3}}\qquad \mathrm{(E) \ } 2a$

Solution

Let the midpoint of $AD$ be $N$. The length of $MN$ is the average of the bases, or $\frac{3a}{2}$. The length of $AN$ is also $\frac{3a}{2}$.

Since $AMN$ is a $45-45-90$ triangle, the length of $AM$ is $\frac{3a}{\sqrt{2}}$, and the answer is $\boxed{\mathrm{B}}$.

See also

2007 Cyprus MO, Lyceum (Problems)
Preceded by
Problem 21 		Followed by
Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2007_Cyprus_MO/Lyceum/Problem_22&oldid=211280"