Difference between revisions of "2007 Cyprus MO/Lyceum/Problem 23"
(problem 23 (without solution)) |
|||
| Line 9: | Line 9: | ||
==Solution== | ==Solution== | ||
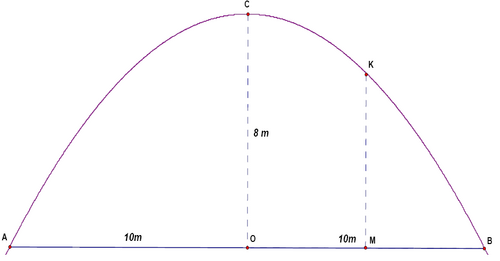
| − | { | + | Since it is a parabolic tunnel, the equation of the tunnel is a quadratic. We have three points: (0,8), (10,0), and (-10,0). Since we have both of the roots, we multiply <math>a(x-10)(x+10)=ax^2-100a</math>. But we also have <math>-100a=8</math>, so <math>a=.08</math>. Thus the equation of the parabola is <math>-.08x^2+8</math>. Now the height of the tunnel at M is the value of the y coordinate when <math>x=5</math>, or <math>6</math>. <math>\mathrm{(E)}</math> |
==See also== | ==See also== | ||
{{CYMO box|year=2007|l=Lyceum|num-b=22|num-a=24}} | {{CYMO box|year=2007|l=Lyceum|num-b=22|num-a=24}} | ||
Latest revision as of 10:31, 12 August 2008
Problem
In the figure above the right section of a parabolic tunnel is presented. Its maximum height is 
and its maximum width is 
. If M is the midpoint of 
, then the height 
of the tunnel at the point 
is
Solution
Since it is a parabolic tunnel, the equation of the tunnel is a quadratic. We have three points: (0,8), (10,0), and (-10,0). Since we have both of the roots, we multiply 
. But we also have 
, so 
. Thus the equation of the parabola is 
. Now the height of the tunnel at M is the value of the y coordinate when 
, or 
. 
See also
| 2007 Cyprus MO, Lyceum (Problems) | ||
| Preceded by Problem 22 |
Followed by Problem 24 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
