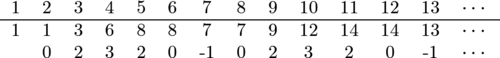Difference between revisions of "2018 AMC 10B Problems/Problem 20"
(→Solution 2 (Bashy Pattern Finding)) |
MRENTHUSIASM (talk | contribs) (→Solution 8) |
||
| (50 intermediate revisions by 11 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{duplicate|[[2018 AMC 12B Problems|2018 AMC 12B #18]] and [[2018 AMC 10B Problems|2018 AMC 10B #20]]}} | ||
| + | |||
==Problem== | ==Problem== | ||
A function <math>f</math> is defined recursively by <math>f(1)=f(2)=1</math> and <cmath>f(n)=f(n-1)-f(n-2)+n</cmath>for all integers <math>n \geq 3</math>. What is <math>f(2018)</math>? | A function <math>f</math> is defined recursively by <math>f(1)=f(2)=1</math> and <cmath>f(n)=f(n-1)-f(n-2)+n</cmath>for all integers <math>n \geq 3</math>. What is <math>f(2018)</math>? | ||
| − | <math>\textbf{(A)} \ | + | <math>\textbf{(A) } 2016 \qquad \textbf{(B) } 2017 \qquad \textbf{(C) } 2018 \qquad \textbf{(D) } 2019 \qquad \textbf{(E) } 2020</math> |
| + | |||
| + | ==Solution 1 (Algebra)== | ||
| + | For all integers <math>n \geq 7,</math> note that | ||
| + | <cmath>\begin{align*} | ||
| + | f(n)&=f(n-1)-f(n-2)+n \\ | ||
| + | &=[f(n-2)-f(n-3)+n-1]-f(n-2)+n \\ | ||
| + | &=-f(n-3)+2n-1 \\ | ||
| + | &=-[f(n-4)-f(n-5)+n-3]+2n-1 \\ | ||
| + | &=-f(n-4)+f(n-5)+n+2 \\ | ||
| + | &=-[f(n-5)-f(n-6)+n-4]+f(n-5)+n+2 \\ | ||
| + | &=f(n-6)+6. | ||
| + | \end{align*}</cmath> | ||
| + | It follows that | ||
| + | <cmath>\begin{align*} | ||
| + | f(2018)&=f(2012)+6 \\ | ||
| + | &=f(2006)+12 \\ | ||
| + | &=f(2000)+18 \\ | ||
| + | & \ \vdots \\ | ||
| + | &=f(2)+2016 \\ | ||
| + | &=\boxed{\textbf{(B) } 2017}. | ||
| + | \end{align*}</cmath> | ||
| + | ~MRENTHUSIASM | ||
| + | |||
| + | ==Solution 2 (Algebra)== | ||
| + | For all integers <math>n\geq3,</math> we rearrange the given equation: <cmath>f(n)-f(n-1)+f(n-2)=n. \hspace{28.25mm}(1)</cmath> | ||
| + | For all integers <math>n\geq4,</math> it follows that <cmath>f(n-1)-f(n-2)+f(n-3)=n-1. \hspace{15mm}(2)</cmath> | ||
| + | For all integers <math>n\geq4,</math> we add <math>(1)</math> and <math>(2):</math> <cmath>f(n)+f(n-3)=2n-1. \hspace{38.625mm}(3)</cmath> | ||
| + | For all integers <math>n\geq7,</math> it follows that <cmath>f(n-3)+f(n-6)=2n-7. \hspace{32mm}(4)</cmath> | ||
| + | For all integers <math>n\geq7,</math> we subtract <math>(4)</math> from <math>(3):</math> <cmath>f(n)-f(n-6)=6. \hspace{47.5mm}(5)</cmath> | ||
| + | From <math>(5),</math> we have the following system of <math>336</math> equations: | ||
| + | <cmath>\begin{align*} | ||
| + | f(2018)-f(2012)&=6, \\ | ||
| + | f(2012)-f(2006)&=6, \\ | ||
| + | f(2006)-f(2000)&=6, \\ | ||
| + | & \ \vdots \\ | ||
| + | f(8)-f(2)&=6. | ||
| + | \end{align*}</cmath> | ||
| + | We add these equations up to get <cmath>f(2018)-f(2)=6\cdot336=2016,</cmath> from which <math>f(2018)=f(2)+2016=\boxed{\textbf{(B) } 2017}.</math> | ||
| + | |||
| + | ~AopsUser101 ~MRENTHUSIASM | ||
| + | |||
| + | ==Solution 3 (Finite Differences)== | ||
| + | |||
| + | Preamble: In this solution, we define the sequence <math>A</math> to satisfy <math>a_n = f(n),</math> where <math>a_n</math> represents the <math>n</math>th term of the sequence <math>A.</math> This solution will show a few different perspectives. Even though it may not be as quick as some of the solutions above, I feel like it is an interesting concept, and may be more motivated. | ||
| + | |||
| + | To begin, we consider the sequence <math>B</math> formed when we take the difference of consecutive terms between <math>A.</math> Define <math>b_n = a_{n+1} - a_n.</math> Notice that for <math>n \ge 4,</math> we have <center><math>\begin{cases}\begin{aligned} a_{n+1} &= a_{n} - a_{n-1} + (n+1) \\ a_{n} &= a_{n-1} - a_{n-2} + n \end{aligned}.\end{cases}</math></center> Notice that subtracting the second equation from the first, we see that <math>b_{n} = b_{n-1} - b_{n-2} + 1.</math> | ||
| − | ==Solution | + | If you didn’t notice that <math>B</math> repeated directly in the solution above, you could also, possibly more naturally, take the finite differences of the sequence <math>b_n</math> so that you could define <math>c_n = b_{n+1} - b_n.</math> Using a similar method as above through reindexing and then subtracting, you could find that <math>c_n = c_{n-1} - c_{n-2}.</math> The sum of any six consecutive terms of a sequence which satisfies such a recursion is <math>0,</math> in which you have that <math>b_{n} = b_{n+6}.</math> In the case in which finite differences didn’t reduce to such a special recursion, you could still find the first few terms of <math>C</math> to see if there are any patterns, now that you have a much simpler sequence. Doing so in this case, it can also be seen by seeing that the sequence <math>C</math> looks like <cmath>\underbrace{2, 1, -1, -2, -1, 1,}_{\text{cycle period}} 2, 1, -1, -2, -1, 1, \ldots</cmath> in which the same result follows. |
| + | |||
| + | Using the fact that <math>B</math> repeats every six terms, this motivates us to look at the sequence <math>B</math> more carefully. Doing so, we see that <math>B</math> looks like <cmath>\underbrace{2, 3, 2, 0, -1, 0,}_{\text{cycle period}} 2, 3, 2, 0, -1, 0, \ldots</cmath> (If you tried pattern finding on sequence <math>B</math> directly, you could also arrive at this result, although I figured defining a second sequence based on finite differences was more motivated.) | ||
| + | |||
| + | Now, there are two ways to finish. | ||
| + | |||
| + | Finish Method #1: Notice that any six consecutive terms of <math>B</math> sum to <math>6,</math> after which we see that <math>a_n = a_{n-6} + 6.</math> Therefore, <math>a_{2018} = a_{2012} + 6 = \cdots = a_{2} + 2016 = \boxed{\textbf{(B) } 2017}.</math> | ||
| + | |||
| + | Finish Method #2: Notice that <math>a_{2018} = a_{2017} - a_{2016} + 2018 = B_{2016} + 2018 = -1 + 2018 = \boxed{\textbf{(B) } 2017}.</math> | ||
| + | |||
| + | ~Professor-Mom | ||
| + | |||
| + | ==Solution 4 (Pattern)== | ||
Start out by listing some terms of the sequence. | Start out by listing some terms of the sequence. | ||
| − | <cmath>f(1)=1</cmath> | + | <cmath>\begin{align*} |
| − | <cmath>f(2)=1</cmath> | + | f(1)&=1 \\ |
| + | f(2)&=1 \\ | ||
| + | f(3)&=3 \\ | ||
| + | f(4)&=6 \\ | ||
| + | f(5)&=8 \\ | ||
| + | f(6)&=8 \\ | ||
| + | f(7)&=7 \\ | ||
| + | f(8)&=7 \\ | ||
| + | f(9)&=9 \\ | ||
| + | f(10)&=12 \\ | ||
| + | f(11)&=14 \\ | ||
| + | f(12)&=14 \\ | ||
| + | f(13)&=13 \\ | ||
| + | f(14)&=13 \\ | ||
| + | f(15)&=15 \\ | ||
| + | & \ \vdots | ||
| + | \end{align*}</cmath> | ||
| + | Notice that <math>f(n)=n</math> whenever <math>n</math> is an odd multiple of <math>3</math>, and the pattern of numbers that follow will always be <math>+2</math>, <math>+3</math>, <math>+2</math>, <math>+0</math>, <math>-1</math>, <math>+0</math>. | ||
| + | The largest odd multiple of <math>3</math> smaller than <math>2018</math> is <math>2013</math>, so we have | ||
| + | <cmath>\begin{align*} | ||
| + | f(2013)&=2013 \\ | ||
| + | f(2014)&=2016 \\ | ||
| + | f(2015)&=2018 \\ | ||
| + | f(2016)&=2018 \\ | ||
| + | f(2017)&=2017 \\ | ||
| + | f(2018)&=\boxed{\textbf{(B) } 2017}. | ||
| + | \end{align*}</cmath> | ||
| + | |||
| + | ==Solution 5 (Pattern)== | ||
| + | Writing out the first few values, we get | ||
| + | <cmath>1,1,3,6,8,8,7,7,9,12,14,14,13,13,15,18,20,20,19,19,\ldots.</cmath> We see that every number <math>x</math> where <math>x \equiv 1\pmod 6</math> has <math>f(x)=x,f(x+1)=f(x)=x,</math> and <math>f(x-1)=f(x-2)=x+1.</math> The greatest number that's <math>1\pmod{6}</math> and less than <math>2018</math> is <math>2017,</math> so we have <math>f(2017)=f(2018)=\boxed{\textbf{(B) } 2017}.</math> | ||
| + | |||
| + | ==Solution 6== | ||
| + | <cmath>\begin{align*} | ||
| + | f(n)&=f(n-1)-f(n-2)+n \\ | ||
| + | f(n-1)&=f(n-2)-f(n-3)+n-1 | ||
| + | \end{align*}</cmath> | ||
| + | Subtracting those two and rearranging gives | ||
| + | <cmath>\begin{align*} | ||
| + | f(n)-2f(n-1)+2f(n-2)-f(n-3)&=1 \\ | ||
| + | f(n-1)-2f(n-2)+2f(n-3)-f(n-4)&=1 | ||
| + | \end{align*}</cmath> | ||
| + | Subtracting those two gives <math>f(n)-3f(n-1)+4f(n-2)-3f(n-3)+f(n-4)=0.</math> | ||
| + | |||
| + | The characteristic polynomial is <math>x^4-3x^3+4x^2-3x+1=0.</math> | ||
| + | |||
| + | <math>x=1</math> is a root, so using synthetic division results in <math>(x-1)(x^3-2x^2+2x-1)=0.</math> | ||
| + | |||
| + | <math>x=1</math> is a root, so using synthetic division results in <math>(x-1)^2(x^2-x+1)=0.</math> | ||
| + | |||
| + | <math>x^2-x+1=0</math> has roots <math>x=\frac{1}{2}\pm\frac{i\sqrt{3}}{2}.</math> | ||
| + | |||
| + | And <cmath>f(n)=(An+D)\cdot1^n+B\cdot\left(\frac{1}{2}-\frac{i\sqrt{3}}{2}\right)^n+C\cdot\left(\frac{1}{2}+\frac{i\sqrt{3}}{2}\right)^n.</cmath> | ||
| + | Plugging in <math>n=1</math>, <math>n=2</math>, <math>n=3</math>, and <math>n=4</math> results in a system of <math>4</math> linear equations<math>\newline</math> | ||
| + | Solving them gives <math>A=1, \ B=\frac{1}{2}-\frac{i\sqrt{3}}{2}, \ C=\frac{1}{2}+\frac{i\sqrt{3}}{2}, \ D=1.</math> Note that you can guess <math>A=1</math> by answer choices. | ||
| + | |||
| + | So plugging in <math>n=2018</math> results in | ||
| + | <cmath>\begin{align*} | ||
| + | 2018+1+\left(\frac{1}{2}-\frac{i\sqrt{3}}{2}\right)^{2019}+\left(\frac{1}{2}+\frac{i\sqrt{3}}{2}\right)^{2019}&=2019+(\cos(-60^{\circ})+\sin(-60^{\circ}))^{2019})+(\cos(60^{\circ})+\sin(60^{\circ}))^{2019}) \\ | ||
| + | &=2019+(\cos(-60^{\circ}\cdot2019)+\sin(-60^{\circ}\cdot2019))+(\cos(60^{\circ}\cdot2019)+sin(60^{\circ}\cdot2019)) \\ | ||
| + | &=\boxed{\textbf{(B) } 2017}. | ||
| + | \end{align*}</cmath> | ||
| + | ~ryanbear | ||
| − | <cmath>f(3)=3 | + | ==Solution 7== |
| − | + | We utilize patterns to solve this equation: | |
| − | + | <cmath>\begin{align*} | |
| − | + | f(3)&=3, \\ | |
| − | + | f(4)&=6, \\ | |
| − | + | f(5)&=8, \\ | |
| + | f(6)&=8, \\ | ||
| + | f(7)&=7, \\ | ||
| + | f(8)&=8. | ||
| + | \end{align*}</cmath> | ||
| + | We realize that the pattern repeats itself. For every six terms, there will be four terms that we repeat, and two terms that we don't repeat. We will exclude the first two for now, because they don't follow this pattern. | ||
| − | < | + | First, we need to know whether or not <math>2016</math> is part of the skip or repeat. We notice that <math>f(6),f(12), \ldots,f(6n)</math> all satisfy <math>6+6(n-1)=n,</math> and we know that <math>2016</math> satisfies this, leaving <math>n=336.</math> Therefore, we know that <math>2016</math> is part of the repeat section. But what number does it repeat? |
| − | < | ||
| − | < | ||
| − | < | ||
| − | < | ||
| − | < | ||
| − | < | + | We know that the repeat period is <math>2,</math> and it follows that pattern of <math>1,1,8,8,7,7.</math> Again, since <math>f(6) = f(5)</math> and so on for the repeat section, <math>f(2016)=f(2015),</math> so we don't need to worry about which one, since it repeats with period <math>2.</math> We see that the repeat pattern of <math>f(6),f(12),\ldots,f(6n)</math> follows <math>8,14,20,</math> it is an arithmetic sequence with common difference <math>6.</math> Therefore, <math>2016</math> is the <math>335</math>th term of this, but including <math>1,</math> it is <math>336\cdot6+1=\boxed{\textbf{(B) } 2017}.</math> |
| − | < | + | |
| − | + | ~CharmaineMa07292010 | |
| − | + | ||
| − | + | ==Solution 8== | |
| − | < | + | |
| − | < | + | We list out the first <math>13</math> terms and their differences: |
| − | < | + | |
| − | < | + | [[File:2018_10b_S8.png|500px|center|Caption for the image]] |
| − | < | + | |
| + | We see the differences are clearly repeating every <math>6</math> terms here; we see that <math>2018\equiv2\pmod6</math>. We see that the values for <math>2</math> and <math>8</math> are both one less, so we conclude our answer is <math>2018-1=\boxed{\textbf{(B)}~2017}.</math> | ||
| + | |||
| + | ~Technodoggo | ||
| + | |||
| + | ==Video Solution== | ||
| − | + | https://www.youtube.com/watch?v=aubDsjVFFTc | |
| − | |||
| − | |||
| − | + | ~bunny1 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | https://youtu.be/ub6CdxulWfc | |
| + | ~savannahsolver | ||
==See Also== | ==See Also== | ||
Latest revision as of 23:02, 7 September 2024
- The following problem is from both the 2018 AMC 12B #18 and 2018 AMC 10B #20, so both problems redirect to this page.
Contents
Problem
A function ![]() is defined recursively by
is defined recursively by ![]() and
and ![]() for all integers
for all integers ![]() . What is
. What is ![]() ?
?
![]()
Solution 1 (Algebra)
For all integers ![]() note that
note that
![\begin{align*} f(n)&=f(n-1)-f(n-2)+n \\ &=[f(n-2)-f(n-3)+n-1]-f(n-2)+n \\ &=-f(n-3)+2n-1 \\ &=-[f(n-4)-f(n-5)+n-3]+2n-1 \\ &=-f(n-4)+f(n-5)+n+2 \\ &=-[f(n-5)-f(n-6)+n-4]+f(n-5)+n+2 \\ &=f(n-6)+6. \end{align*}](http://latex.artofproblemsolving.com/f/2/1/f2105fca2047fe7c4dfa2f0d1a0ed4cd534ca771.png) It follows that
It follows that
 ~MRENTHUSIASM
~MRENTHUSIASM
Solution 2 (Algebra)
For all integers ![]() we rearrange the given equation:
we rearrange the given equation: ![]() For all integers
For all integers ![]() it follows that
it follows that ![]() For all integers
For all integers ![]() we add
we add ![]() and
and ![]()
![]() For all integers
For all integers ![]() it follows that
it follows that ![]() For all integers
For all integers ![]() we subtract
we subtract ![]() from
from ![]()
![]() From
From ![]() we have the following system of
we have the following system of ![]() equations:
equations:
 We add these equations up to get
We add these equations up to get ![]() from which
from which ![]()
~AopsUser101 ~MRENTHUSIASM
Solution 3 (Finite Differences)
Preamble: In this solution, we define the sequence ![]() to satisfy
to satisfy ![]() where
where ![]() represents the
represents the ![]() th term of the sequence
th term of the sequence ![]() This solution will show a few different perspectives. Even though it may not be as quick as some of the solutions above, I feel like it is an interesting concept, and may be more motivated.
This solution will show a few different perspectives. Even though it may not be as quick as some of the solutions above, I feel like it is an interesting concept, and may be more motivated.
To begin, we consider the sequence ![]() formed when we take the difference of consecutive terms between
formed when we take the difference of consecutive terms between ![]() Define
Define ![]() Notice that for
Notice that for ![]() we have
we have
Notice that subtracting the second equation from the first, we see that ![]()
If you didn’t notice that ![]() repeated directly in the solution above, you could also, possibly more naturally, take the finite differences of the sequence
repeated directly in the solution above, you could also, possibly more naturally, take the finite differences of the sequence ![]() so that you could define
so that you could define ![]() Using a similar method as above through reindexing and then subtracting, you could find that
Using a similar method as above through reindexing and then subtracting, you could find that ![]() The sum of any six consecutive terms of a sequence which satisfies such a recursion is
The sum of any six consecutive terms of a sequence which satisfies such a recursion is ![]() in which you have that
in which you have that ![]() In the case in which finite differences didn’t reduce to such a special recursion, you could still find the first few terms of
In the case in which finite differences didn’t reduce to such a special recursion, you could still find the first few terms of ![]() to see if there are any patterns, now that you have a much simpler sequence. Doing so in this case, it can also be seen by seeing that the sequence
to see if there are any patterns, now that you have a much simpler sequence. Doing so in this case, it can also be seen by seeing that the sequence ![]() looks like
looks like ![]() in which the same result follows.
in which the same result follows.
Using the fact that ![]() repeats every six terms, this motivates us to look at the sequence
repeats every six terms, this motivates us to look at the sequence ![]() more carefully. Doing so, we see that
more carefully. Doing so, we see that ![]() looks like
looks like ![]() (If you tried pattern finding on sequence
(If you tried pattern finding on sequence ![]() directly, you could also arrive at this result, although I figured defining a second sequence based on finite differences was more motivated.)
directly, you could also arrive at this result, although I figured defining a second sequence based on finite differences was more motivated.)
Now, there are two ways to finish.
Finish Method #1: Notice that any six consecutive terms of ![]() sum to
sum to ![]() after which we see that
after which we see that ![]() Therefore,
Therefore, ![]()
Finish Method #2: Notice that ![]()
~Professor-Mom
Solution 4 (Pattern)
Start out by listing some terms of the sequence.
 Notice that
Notice that ![]() whenever
whenever ![]() is an odd multiple of
is an odd multiple of ![]() , and the pattern of numbers that follow will always be
, and the pattern of numbers that follow will always be ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
The largest odd multiple of
.
The largest odd multiple of ![]() smaller than
smaller than ![]() is
is ![]() , so we have
, so we have

Solution 5 (Pattern)
Writing out the first few values, we get
![]() We see that every number
We see that every number ![]() where
where ![]() has
has ![]() and
and ![]() The greatest number that's
The greatest number that's ![]() and less than
and less than ![]() is
is ![]() so we have
so we have ![]()
Solution 6
![]() Subtracting those two and rearranging gives
Subtracting those two and rearranging gives
![]() Subtracting those two gives
Subtracting those two gives ![]()
The characteristic polynomial is ![]()
![]() is a root, so using synthetic division results in
is a root, so using synthetic division results in ![]()
![]() is a root, so using synthetic division results in
is a root, so using synthetic division results in ![]()
![]() has roots
has roots ![]()
And ![\[f(n)=(An+D)\cdot1^n+B\cdot\left(\frac{1}{2}-\frac{i\sqrt{3}}{2}\right)^n+C\cdot\left(\frac{1}{2}+\frac{i\sqrt{3}}{2}\right)^n.\]](http://latex.artofproblemsolving.com/c/d/f/cdfdf672769eb54ec37e45d7299adc8e732be5ed.png) Plugging in
Plugging in ![]() ,
, ![]() ,
, ![]() , and
, and ![]() results in a system of
results in a system of ![]() linear equations
linear equations![]() Solving them gives
Solving them gives ![]() Note that you can guess
Note that you can guess ![]() by answer choices.
by answer choices.
So plugging in ![]() results in
results in
 ~ryanbear
~ryanbear
Solution 7
We utilize patterns to solve this equation:
 We realize that the pattern repeats itself. For every six terms, there will be four terms that we repeat, and two terms that we don't repeat. We will exclude the first two for now, because they don't follow this pattern.
We realize that the pattern repeats itself. For every six terms, there will be four terms that we repeat, and two terms that we don't repeat. We will exclude the first two for now, because they don't follow this pattern.
First, we need to know whether or not ![]() is part of the skip or repeat. We notice that
is part of the skip or repeat. We notice that ![]() all satisfy
all satisfy ![]() and we know that
and we know that ![]() satisfies this, leaving
satisfies this, leaving ![]() Therefore, we know that
Therefore, we know that ![]() is part of the repeat section. But what number does it repeat?
is part of the repeat section. But what number does it repeat?
We know that the repeat period is ![]() and it follows that pattern of
and it follows that pattern of ![]() Again, since
Again, since ![]() and so on for the repeat section,
and so on for the repeat section, ![]() so we don't need to worry about which one, since it repeats with period
so we don't need to worry about which one, since it repeats with period ![]() We see that the repeat pattern of
We see that the repeat pattern of ![]() follows
follows ![]() it is an arithmetic sequence with common difference
it is an arithmetic sequence with common difference ![]() Therefore,
Therefore, ![]() is the
is the ![]() th term of this, but including
th term of this, but including ![]() it is
it is ![]()
~CharmaineMa07292010
Solution 8
We list out the first ![]() terms and their differences:
terms and their differences:
We see the differences are clearly repeating every ![]() terms here; we see that
terms here; we see that ![]() . We see that the values for
. We see that the values for ![]() and
and ![]() are both one less, so we conclude our answer is
are both one less, so we conclude our answer is ![]()
~Technodoggo
Video Solution
https://www.youtube.com/watch?v=aubDsjVFFTc
~bunny1
~savannahsolver
See Also
| 2018 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 19 |
Followed by Problem 21 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2018 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 17 |
Followed by Problem 19 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.