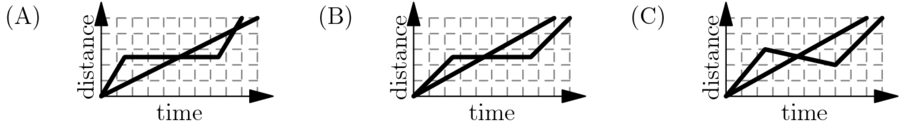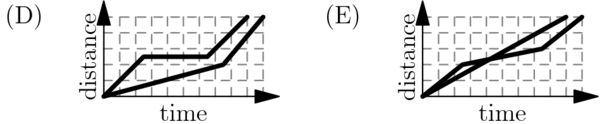2019 AMC 8 Problems/Problem 5
Contents
[hide]Problem 5
A tortoise challenges a hare to a race. The hare eagerly agrees and quickly runs ahead, leaving the slow-moving tortoise behind. Confident that he will win, the hare stops to take a nap. Meanwhile, the tortoise walks at a slow steady pace for the entire race. The hare awakes and runs to the finish line, only to find the tortoise already there. Which of the following graphs matches the description of the race, showing the distance ![]() traveled by the two animals over time
traveled by the two animals over time ![]() from start to finish?
from start to finish?
Solution 1
First, the tortoise walks at a constant rate, ruling out ![]() Second, when the hare is resting, the distance will stay the same, ruling out
Second, when the hare is resting, the distance will stay the same, ruling out ![]() and
and ![]() .
Third, the tortoise wins the race, meaning that the non-constant one should go off the graph last, ruling out
.
Third, the tortoise wins the race, meaning that the non-constant one should go off the graph last, ruling out ![]() .
Therefore, the answer
.
Therefore, the answer ![]() is the only one left.
is the only one left.
![]()
Solution 2
First, we know that the rabbit beats the tortoise in the first half of the race. So he is going to be ahead of the tortoise. We also know, while he rested, he didn't move. The only graph portraying that is going to be ![]() . This is our answer. Just remember, since the tortoise finished faster than the hare, his line will be a lesser value on the time-axis. ~bobthefam, Edited by Rishi09
. This is our answer. Just remember, since the tortoise finished faster than the hare, his line will be a lesser value on the time-axis. ~bobthefam, Edited by Rishi09
Video Solution
The Learning Royal: https://youtu.be/IiFFDDITE6Q
Video Solution 2
Solution detailing how to solve the problem: https://www.youtube.com/watch?v=uQTM8Kmh9B8&list=PLbhMrFqoXXwmwbk2CWeYOYPRbGtmdPUhL&index=6
Video Solution 3
~savannahsolver
See also
| 2019 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 4 |
Followed by Problem 6 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()