1994 AHSME Problems/Problem 28
Contents
[hide]Problem
In the ![]() -plane, how many lines whose
-plane, how many lines whose ![]() -intercept is a positive prime number and whose
-intercept is a positive prime number and whose ![]() -intercept is a positive integer pass through the point
-intercept is a positive integer pass through the point ![]() ?
?
![]()
Solution 1
The line with ![]() -intercept
-intercept ![]() and
and ![]() -intercept
-intercept ![]() is given by the equation
is given by the equation ![]() . We are told
. We are told ![]() is on the line so
is on the line so
![]()
Since ![]() and
and ![]() are integers, this equation holds only if
are integers, this equation holds only if ![]() is a factor of
is a factor of ![]() . The factors are
. The factors are ![]() which means
which means ![]() must be one of
must be one of ![]() . The only members of this list which are prime are
. The only members of this list which are prime are ![]() and
and ![]() , so the number of solutions is
, so the number of solutions is ![]() .
.
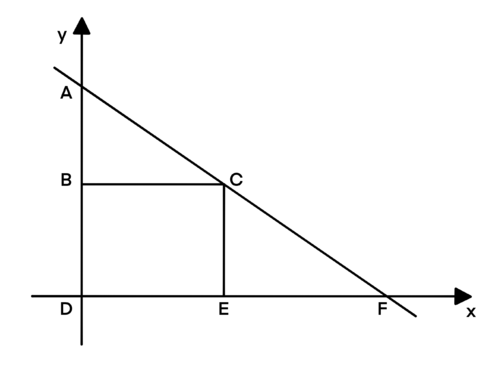
Solution 2
Let ![]() ,
, ![]() , and
, and ![]() . As stated in the problem, the
. As stated in the problem, the ![]() -intercept
-intercept ![]() is a positive prime number, and the
is a positive prime number, and the ![]() -intercept
-intercept ![]() is a positive integer.
is a positive integer.
Through similar triangles, ![]() ,
, ![]() ,
, ![]()
The only cases where ![]() is prime are:
is prime are:
![\[\begin{cases} a-4=1 & a=5 \\ b-3=12 & b=15 \end{cases}\]](http://latex.artofproblemsolving.com/0/c/a/0cac85b866ec5f0657b04e3c17ce9e8c4bb36fe3.png)
![]()
![\[\begin{cases} a-4=3 & a=7 \\ b-3=4 & b=5 \end{cases}\]](http://latex.artofproblemsolving.com/3/0/8/3089bf447d47f45d44563da32f68bbcadb7749b4.png)
So the number of solutions are ![]() .
.
See Also
| 1994 AHSME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 27 |
Followed by Problem 29 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
| All AHSME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()