2021 AMC 12A Problems/Problem 24
Contents
[hide]- 1 Problem
- 2 Diagram
- 3 Solution 1 (Possible Without Trigonometry)
- 4 Solution 2 (Trigonometry)
- 5 Solution 3 (Weighted Averages and Similar Triangles)
- 6 Solution 4 (Similar Triangles)
- 7 Solution 5 (Law of Sine and Power of a Point)
- 8 Solution 6 (Analytic Geometry)
- 9 Video Solution by MOP 2024
- 10 Video Solution by Punxsutawney Phil
- 11 Video Solution by OmegaLearn (Similar Triangles, Law of Sines, Law of Cosines )
- 12 Video Solution
- 13 See also
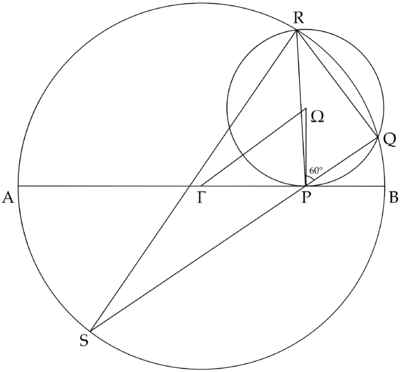
Problem
Semicircle ![]() has diameter
has diameter ![]() of length
of length ![]() . Circle
. Circle ![]() lies tangent to
lies tangent to ![]() at a point
at a point ![]() and intersects
and intersects ![]() at points
at points ![]() and
and ![]() . If
. If ![]() and
and ![]() , then the area of
, then the area of ![]() equals
equals ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers, and
are relatively prime positive integers, and ![]() is a positive integer not divisible by the square of any prime. What is
is a positive integer not divisible by the square of any prime. What is ![]() ?
?
![]()
Diagram
![[asy] /* Made by MRENTHUSIASM */ size(300); pair O, X, A, B, P, Q, R; O = (0,0); X = (4,3); A = (-7,0); B = (7,0); P = (4,0); Q = intersectionpoints(Circle(O,7),Circle(X,3))[0]; R = intersectionpoints(Circle(O,7),Circle(X,3))[1]; filldraw(P--Q--R--cycle,yellow); dot("$\Gamma$",O,S); dot("$\Omega$",X,E); dot("$A$",A,SW); dot("$B$",B,SE); dot("$P$",P,S); dot("$Q$",Q,E); dot("$R$",R,N); draw(arc(O, 7, 0, 180)^^A--B^^Circle(X,3)); [/asy]](http://latex.artofproblemsolving.com/d/1/4/d1437a196444ca0e708a42560c79be6ef326fac9.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution 1 (Possible Without Trigonometry)
Let ![]() be the center of the semicircle and
be the center of the semicircle and ![]() be the center of the circle.
be the center of the circle.
Applying the Extended Law of Sines to ![]() we find the radius of
we find the radius of ![]()
![\[XP=\frac{QR}{2\cdot\sin \angle QPR}=\frac{3\sqrt3}{2\cdot\frac{\sqrt3}{2}}=3.\]](http://latex.artofproblemsolving.com/7/5/c/75c0fd0a48572595a8b4a9295261b6ffe02f5fc1.png) Alternatively, by the Inscribed Angle Theorem,
Alternatively, by the Inscribed Angle Theorem, ![]() is a
is a ![]() triangle with base
triangle with base ![]() Dividing
Dividing ![]() into two congruent
into two congruent ![]() triangles, we get that the radius of
triangles, we get that the radius of ![]() is
is ![]() by the side-length ratios.
by the side-length ratios.
Let ![]() be the midpoint of
be the midpoint of ![]() By the Perpendicular Chord Bisector Converse, we have
By the Perpendicular Chord Bisector Converse, we have ![]() and
and ![]() Together, points
Together, points ![]() and
and ![]() must be collinear.
must be collinear.
By the SAS Congruence, we have ![]() both of which are
both of which are ![]() triangles. By the side-length ratios, we obtain
triangles. By the side-length ratios, we obtain ![]() and
and ![]() By the Pythagorean Theorem on right
By the Pythagorean Theorem on right ![]() we get
we get ![]() and
and ![]() By the Pythagorean Theorem on right
By the Pythagorean Theorem on right ![]() we get
we get ![]()
Let ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() and
and ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() as shown below:
as shown below:
![[asy] /* Made by MRENTHUSIASM */ size(300); pair O, X, A, B, P, Q, R, M, C, D; O = (0,0); X = (4,3); A = (-7,0); B = (7,0); P = (4,0); Q = intersectionpoints(Circle(O,7),Circle(X,3))[0]; R = intersectionpoints(Circle(O,7),Circle(X,3))[1]; M = midpoint(Q--R); C = foot(P,Q,R); D = foot(X,P,C); fill(P--Q--R--cycle,yellow); dot("$O$",O,S); dot("$X$",X,N); dot("$A$",A,SW); dot("$B$",B,SE); dot("$P$",P,S); dot("$Q$",Q,E); dot("$R$",R,N); dot("$M$",M,dir(M)); dot("$C$",C,NE); dot("$D$",D,SE); markscalefactor=0.0375; draw(rightanglemark(O,M,R),red); draw(rightanglemark(P,C,M),red); draw(rightanglemark(P,D,X),red); draw(rightanglemark(O,P,X),red); draw(P--Q--R--cycle); draw(arc(O, 7, 0, 180)^^A--B^^Circle(X,3)); draw(O--M^^X--P); draw(P--C^^X--D,dashed); [/asy]](http://latex.artofproblemsolving.com/f/b/6/fb6903e700afabd6b0aa4eacb66286e7f5a760f5.png) Clearly, quadrilateral
Clearly, quadrilateral ![]() is a rectangle. Since
is a rectangle. Since ![]() by alternate interior angles, we have
by alternate interior angles, we have ![]() by the AA Similarity, with the ratio of similitude
by the AA Similarity, with the ratio of similitude ![]() Therefore, we get
Therefore, we get ![]() and
and ![]()
The area of ![]() is
is ![]() from which the answer is
from which the answer is ![]()
~MRENTHUSIASM
Solution 2 (Trigonometry)
![[asy] size(150); draw(circle((7,0),7)); pair A = (0, 0); pair B = (14, 0); draw(A--B); draw(circle((11,3),3)); label("$C$", (7, 0), S); label("$O$", (11, 3), E); label("$P$", (11, 0), S); pair C = (7, 0); pair O = (11, 3); pair P = (11, 0); pair Q = intersectionpoints(circle(C, 7), circle(O, 3))[1]; pair R = intersectionpoints(circle(C, 7), circle(O, 3))[0]; draw(C--O); draw(C--Q); draw(C--R); draw(Q--R); draw(O--P); draw(O--Q); draw(O--R); draw(P--Q); draw(P--R); label("$Q$", Q, N); label("$R$", R, E); [/asy]](http://latex.artofproblemsolving.com/c/a/4/ca46a45b0c50cbfd6f1009d13785eb71204b9c1d.png)
Suppose we label the points as shown in the diagram above, where ![]() is the center of the semicircle and
is the center of the semicircle and ![]() is the center of the circle tangent to
is the center of the circle tangent to ![]() . Since
. Since ![]() , we have
, we have ![]() and
and ![]() is a
is a ![]() triangle, which can be split into two
triangle, which can be split into two ![]() triangles by the altitude from
triangles by the altitude from ![]() . Since
. Since ![]() we know
we know ![]() by
by ![]() triangles. The area of this part of
triangles. The area of this part of ![]() is
is ![]() . We would like to add this value to the sum of the areas of the other two parts of
. We would like to add this value to the sum of the areas of the other two parts of ![]() .
.
To find the areas of the other two parts of ![]() using the
using the ![]() area formula, we need the sides and included angles. Here we know the sides but what we don't know are the angles. So it seems like we will have to use an angle from another triangle and combine them with the angles we already know to find these angles easily. We know that
area formula, we need the sides and included angles. Here we know the sides but what we don't know are the angles. So it seems like we will have to use an angle from another triangle and combine them with the angles we already know to find these angles easily. We know that ![]() and triangles
and triangles ![]() and
and ![]() are congruent as they share a side,
are congruent as they share a side, ![]() and
and ![]() . Therefore
. Therefore ![]() . Suppose
. Suppose ![]() . Then
. Then ![]() , and since
, and since ![]() , this simplifies to
, this simplifies to ![]() . This factors nicely as
. This factors nicely as ![]() , so
, so ![]() as
as ![]() can't be
can't be ![]() . Since
. Since ![]() and
and ![]() , we now know that
, we now know that ![]() is a
is a ![]() right triangle. This may be useful info for later as we might use an angle in this triangle to find the areas of the other two parts of
right triangle. This may be useful info for later as we might use an angle in this triangle to find the areas of the other two parts of ![]() .
.
Let ![]() . Then
. Then ![]() and
and ![]() . The sum of the areas of
. The sum of the areas of ![]() and
and ![]() is
is ![]() which we will add to
which we will add to ![]() to get the area of
to get the area of ![]() . Observe that
. Observe that ![]() and similarly
and similarly ![]() . Adding these two gives
. Adding these two gives ![]() and multiplying that by
and multiplying that by ![]() gets us
gets us ![]() which we add to
which we add to ![]() to get
to get ![]() . The answer is
. The answer is ![]()
~sugar_rush
Solution 3 (Weighted Averages and Similar Triangles)
![[asy] size(300); pair C = (7, 0); draw(arc(C, 7, 0, 180)); pair A = (0, 0), B = (14, 0); draw(A--B); draw(circle((11,3),3)); label("$A$", A, SSE); label("$B$", B, SSW); label("$C$", (A+B)/2, S); label("$O$", (11, 3), E); label("$P$", (11, 0), S); pair O = (11, 3), P = (11, 0), Q = intersectionpoints(circle(C, 7), circle(O, 3))[1], R = intersectionpoints(circle(C, 7), circle(O, 3))[0], S = (Q+R)/2, N = (121/8, 0), T = (8/11)*N + (3/11)*R, X = (4/7)*T + (3/7)*S; draw(C--O, blue); draw(O--S, red); draw(C--Q); draw(C--R); draw(Q--N--B); draw(O--P); draw(O--Q); draw(O--R); draw(P--Q--R--cycle); draw(B--T); draw(P--X); label("$Q$", Q, NNE); label("$R$", R, E); label("$S$", S, ENE); label("$N$", N, SSE); label("$T$", T, ENE); label("$X$", X, NE); draw(rightanglemark(P, X, Q)); draw(rightanglemark(B, T, R)); draw(rightanglemark(C, S, Q)); [/asy]](http://latex.artofproblemsolving.com/b/4/b/b4bd3b928b572ed1edf564ae1c683c8fffd19cdd.png) Define points as shown above, where
Define points as shown above, where ![]() . The area of
. The area of ![]() is simply
is simply![]() it remains to compute the value of
it remains to compute the value of ![]() . Note that
. Note that ![]() is simply a weighted average of
is simply a weighted average of ![]() and
and ![]() it is
it is ![]() times closer to
times closer to ![]() than it is to
than it is to ![]() . Observe that
. Observe that![\[CS=\sqrt{CQ^{2}-\left(\dfrac{1}{2}QR\right)^{2}}=\sqrt{7^{2}-\left(\dfrac{3\sqrt{3}}{2}\right)^{2}}=6.5\]](http://latex.artofproblemsolving.com/9/4/a/94ab7413cf5b9c75de5c5387284fae0906c58b01.png) since the radius of
since the radius of ![]() is
is ![]() as its diameter is
as its diameter is ![]() . Note also by the Extended Law of Sines the radius of
. Note also by the Extended Law of Sines the radius of ![]() is
is ![]() so
so ![]() . Since
. Since ![]() and
and ![]() are collinear by symmetry we have
are collinear by symmetry we have ![]() so
so ![]() and
and ![]() . Therefore,
. Therefore, ![]() is a
is a ![]() right triangle;
right triangle; ![]() since
since ![]() and
and ![]() . Therefore
. Therefore ![]() so
so ![]() . Since
. Since ![]() we have
we have ![]() . Therefore
. Therefore ![]() so
so ![]() is
is ![]() times as close to
times as close to ![]() as to
as to ![]() we can compute
we can compute ![]() . The area of
. The area of ![]() is
is![]() and
and ![]() .
.
~sugar_rush
Solution 4 (Similar Triangles)
Let ![]() be the center of
be the center of ![]() be the center of
be the center of ![]() and
and ![]() be the midpoint of
be the midpoint of ![]() We have
We have  and by Extended Law of Sines, the radius of
and by Extended Law of Sines, the radius of ![]() is
is ![]() so
so ![]() Therefore
Therefore ![]() and
and ![]()
Let ![]() Obviously
Obviously ![]() so
so ![]() with ratio
with ratio ![]() Therefore
Therefore ![]() and
and ![]()
Let ![]() denote the foot of the altitude from
denote the foot of the altitude from ![]() to
to ![]() Because
Because ![]() it follows that
it follows that ![]() This similarity has ratio
This similarity has ratio ![]() We therefore have
We therefore have ![]()
Finally, the area of ![]() is
is ![]() so the answer is
so the answer is ![]()
~inventivedant
Solution 5 (Law of Sine and Power of a Point)
By the Law of Sine in ![]() and its circumcircle
and its circumcircle ![]() ,
,  ,
, ![]()
![\[\Gamma \Omega = \sqrt{r_{\Gamma}^2 - \left( \frac{ QR }{2}\right)^2} - \sqrt{r_{\Omega}^2 - \left( \frac{QR}{2}\right)^2} = \sqrt{7^2 - \left( \frac{ 3 \sqrt{3} }{2}\right)^2} - \sqrt{3^2 - \left( \frac{ 3 \sqrt{3} }{2}\right)^2} = \frac{13}{2} - \frac32 = 5, \quad \Gamma P = \sqrt{5^2 - 3^2} = 4\]](http://latex.artofproblemsolving.com/2/4/7/2471054db0758bd0fe6ab4c54946d4d5ea1abd6e.png)
By Power of a Point in ![]() ,
, ![]() .
.
By the Law of Sine in ![]() ,
, ![]()
By the Law of Sine in ![]() and its circumcircle
and its circumcircle ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
![\[\frac{PR}{PS} = \frac{ \frac{ 3\sqrt{3} }{14} }{ \frac{ 5\sqrt{3} }{14} } = \frac35, \quad PQ \cdot PR = PQ \cdot PS \cdot \frac{PR}{PS} = 33 \cdot \frac35 = \frac{99}{5}\]](http://latex.artofproblemsolving.com/9/7/7/9776ddd3e28d65adc83341e500ecf7dd54155ecc.png)
![]()
Solution 6 (Analytic Geometry)
Following Solution 4, We have ![]() (0,0) ,
(0,0) , ![]() (4,3).
We can write the equation of the two circles as:
(4,3).
We can write the equation of the two circles as: ![]()
![]() By substituting (1) into (2), we get
By substituting (1) into (2), we get ![]() Notice (3) is the relationship between
Notice (3) is the relationship between ![]() value and
value and ![]() value, in other words, (3) is the linear equation that go through
value, in other words, (3) is the linear equation that go through ![]() and
and ![]() .
Let the height drops from
.
Let the height drops from ![]() to
to ![]() at
at ![]() . Therefore, we have
. Therefore, we have ![]() So
So ![]() And by distance formula,
And by distance formula, ![]() is the distance from
is the distance from ![]() (4,0) to
(4,0) to ![]() .
. ![]() Thus, We get
Thus, We get ![]() So the answer is
So the answer is ![]()
~ERiccc
Video Solution by MOP 2024
https://youtube.com/watch?v=UJ_M_cjul1Q
~r00tsOfUnity
Video Solution by Punxsutawney Phil
https://youtube.com/watch?v=cEHF5iWMe9c
This is invalid. ~r00tsOfUnity
Video Solution by OmegaLearn (Similar Triangles, Law of Sines, Law of Cosines )
~pi_is_3.14
Video Solution
~MathProblemSolvingSkills.com
See also
| 2021 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 23 |
Followed by Problem 25 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()