Difference between revisions of "2002 AMC 12B Problems/Problem 14"
A1337h4x0r (talk | contribs) (→Solution 2) |
A1337h4x0r (talk | contribs) (→Solution 3) |
||
| Line 19: | Line 19: | ||
==Solution 3== | ==Solution 3== | ||
| − | Pick a circle any circle-<math>4</math> ways. Then, pick any other circle-<math>3</math> ways. For each of these circles, there will be 2 intersections, for a total of <math>4*3*2</math> = <math>24</math> intersections. However, we have counted each intersection twice, so we divide for overcounting. Therefore, we reach a total of <math>\frac{24}{2}=\boxed{12}</math>, which corresponds to <math>\text{(D)}</math>. | + | Pick a circle any circle- <math>4</math> ways. Then, pick any other circle- <math>3</math> ways. For each of these circles, there will be 2 intersections, for a total of <math>4*3*2</math> = <math>24</math> intersections. However, we have counted each intersection twice, so we divide for overcounting. Therefore, we reach a total of <math>\frac{24}{2}=\boxed{12}</math>, which corresponds to <math>\text{(D)}</math>. |
== See also == | == See also == | ||
Revision as of 12:18, 30 November 2019
- The following problem is from both the 2002 AMC 12B #14 and 2002 AMC 10B #18, so both problems redirect to this page.
Problem
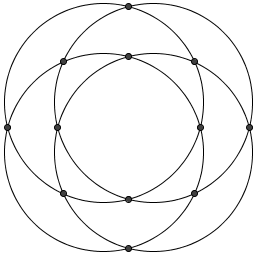
Four distinct circles are drawn in a plane. What is the maximum number of points where at least two of the circles intersect?
Solution 1
For any given pair of circles, they can intersect at most 
times. Since there are 
pairs of circles, the maximum number of possible intersections is 
. We can construct such a situation as below, so the answer is 
.
Solution 2
Because a pair or circles can intersect at most times, the first circle can intersect the second at points, the third can intersect the first two at 
points, and the fourth can intersect the first three at 
points. This means that our answer is 
Solution 3
Pick a circle any circle- ways. Then, pick any other circle- 
ways. For each of these circles, there will be 2 intersections, for a total of 
= 
intersections. However, we have counted each intersection twice, so we divide for overcounting. Therefore, we reach a total of 
, which corresponds to 
.
See also
| 2002 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 17 |
Followed by Problem 19 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2002 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 13 |
Followed by Problem 15 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
