Difference between revisions of "1995 AIME Problems"
| Line 13: | Line 13: | ||
== Problem 3 == | == Problem 3 == | ||
| + | Starting at <math>\displaystyle (0,0),</math> an object moves in the coordinate plane via a sequence of steps, each of length one. Each step is left, right, up, or down, all four equally likely. Let <math>\displaystyle p</math> be the probability that the object reaches <math>\displaystyle (2,2)</math> in six or fewer steps. Given that <math>\displaystyle p</math> can be written in the form <math>\displaystyle m/n,</math> where <math>\displaystyle m</math> and <math>\displaystyle n</math> are relatively prime positive integers, find <math>\displaystyle m+n.</math> | ||
[[1995 AIME Problems/Problem 3|Solution]] | [[1995 AIME Problems/Problem 3|Solution]] | ||
Revision as of 21:58, 21 January 2007
Contents
[hide]Problem 1
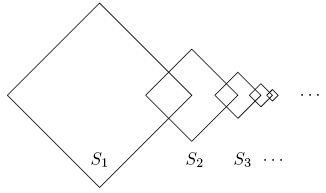
Square ![]() is
is ![]() For
For ![]() the lengths of the sides of square
the lengths of the sides of square ![]() are half the lengths of the sides of square
are half the lengths of the sides of square ![]() two adjacent sides of square
two adjacent sides of square ![]() are perpendicular bisectors of two adjacent sides of square
are perpendicular bisectors of two adjacent sides of square ![]() and the other two sides of square
and the other two sides of square ![]() are the perpendicular bisectors of two adjacent sides of square
are the perpendicular bisectors of two adjacent sides of square ![]() The total area enclosed by at least one of
The total area enclosed by at least one of ![]() can be written in the form
can be written in the form ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 2
Find the last three digits of the product of the positive roots of
![]()
Problem 3
Starting at ![]() an object moves in the coordinate plane via a sequence of steps, each of length one. Each step is left, right, up, or down, all four equally likely. Let
an object moves in the coordinate plane via a sequence of steps, each of length one. Each step is left, right, up, or down, all four equally likely. Let ![]() be the probability that the object reaches
be the probability that the object reaches ![]() in six or fewer steps. Given that
in six or fewer steps. Given that ![]() can be written in the form
can be written in the form ![]() where
where ![]() and
and ![]() are relatively prime positive integers, find
are relatively prime positive integers, find ![]()