Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1999 AIME Problems/Problem 6"

(solution by ginaboys)
 
(10 intermediate revisions by 8 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
A transformation of the first quadrant of the coordinate plane maps each point <math>(x,y)</math> to the point <math>(\sqrt{x},\sqrt{y}).</math>  The vertices of quadrilateral <math>ABCD</math> are <math>A=(900,300), B=(1800,600), C=(600,1800),</math> and <math>D=(300,900).</math>  Let <math>k_{}</math> be the area of the region enclosed by the image of quadrilateral <math>ABCD.</math>  Find the greatest integer that does not exceed <math>k_{}.</math>
+
A transformation of the first [[quadrant]] of the [[coordinate plane]] maps each point <math>(x,y)</math> to the point <math>(\sqrt{x},\sqrt{y}).</math>  The [[vertex|vertices]] of [[quadrilateral]] <math>ABCD</math> are <math>A=(900,300), B=(1800,600), C=(600,1800),</math> and <math>D=(300,900).</math>  Let <math>k_{}</math> be the area of the region enclosed by the image of quadrilateral <math>ABCD.</math>  Find the greatest integer that does not exceed <math>k_{}.</math>
  
−
== Solution ==
+
==Solution==
−
<cmath>\begin{eqnarray*}A' && (\sqrt {900}, \sqrt {300})\\
+
<cmath>\begin{eqnarray*}A' = & (\sqrt {900}, \sqrt {300})\\
−
B' && (\sqrt {1800}, \sqrt {600})\\
+
B' = & (\sqrt {1800}, \sqrt {600})\\
−
C' && (\sqrt {600}, \sqrt {1800})\\
+
C' = & (\sqrt {600}, \sqrt {1800})\\
−
D' && (\sqrt {300}, \sqrt {900}) \end{eqnarray*}</cmath>
+
D' = & (\sqrt {300}, \sqrt {900}) \end{eqnarray*}</cmath>
  
−
First we see that lines passing through <math>AB</math> and <math>CD</math> have equations <math>y = \frac {1}{3}x</math> and <math>y = 3x</math>, respectively. Looking at the points above, we see the equations for <math>A'B'</math> and <math>C'D'</math> are <math>y^2 = \frac {1}{3}x^2</math> and <math>y^2 = 3x^2</math>, or, after manipulation <math>y = \frac {x}{\sqrt {3}}</math> and <math>y = \sqrt {3}x</math>, respectively, which are still linear functions. Basically the square of the image points give back the original points and we could plug them back into the original equation to get the equation of the image lines.  
+
First we see that lines passing through <math>AB</math> and <math>CD</math> have [[equation]]s <math>y = \frac {1}{3}x</math> and <math>y = 3x</math>, respectively. Looking at the points above, we see the equations for <math>A'B'</math> and <math>C'D'</math> are <math>y^2 = \frac {1}{3}x^2</math> and <math>y^2 = 3x^2</math>, or, after manipulation <math>y = \frac {x}{\sqrt {3}}</math> and <math>y = \sqrt {3}x</math>, respectively, which are still linear functions. Basically the square of the image points gives back the original points and we could plug them back into the original equation to get the equation of the image lines.  
  
−
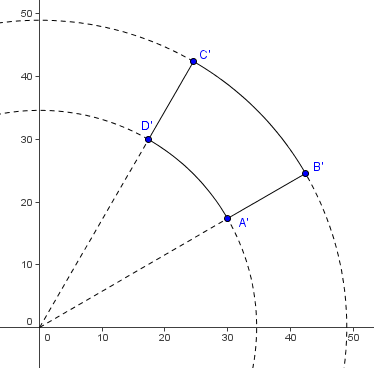
Now take a look at <math>BC</math> and <math>AD</math>, which have the quations <math>y = - x + 2400</math> and <math>y = - x + 1200</math>. The image equations hence are <math>x^2 + y^2 = 2400</math> and <math>x^2 + y^2 = 1200</math>, respectively, which are the equations for circles.  
+
Now take a look at <math>BC</math> and <math>AD</math>, which have the equations <math>y = - x + 2400</math> and <math>y = - x + 1200</math>. The image equations hence are <math>x^2 + y^2 = 2400</math> and <math>x^2 + y^2 = 1200</math>, respectively, which are the equations for [[circle]]s.  
  
 
[[Image:1999_AIME-6.png]]
 
[[Image:1999_AIME-6.png]]
  
−
To find the area between the circles (actually, parts of the circles), we need to figure out the angle of the arc. This could be done by <math>\arctan \sqrt {3} - \arctan \frac {1}{\sqrt {3}} = 60^\circ - 30^\circ = 30^\circ</math>. So the requested areas is the area of the enclosed part of the smaller circle subtracted from the area enclosed by the part of the larger circle = <math>\frac {30^\circ}{360^\circ}(R\pi - r\pi) = \frac {1}{12}(2400\pi - 1200\pi) = 100\pi</math>. Hence the answer is <math>\boxed{314}</math>.
+
To find the area between the circles (actually, parts of the circles), we need to figure out the [[angle]] of the [[arc]]. This could be done by <math>\arctan \sqrt {3} - \arctan \frac {1}{\sqrt {3}} = 60^\circ - 30^\circ = 30^\circ</math>. So the requested areas are the area of the enclosed part of the smaller circle subtracted from the area enclosed by the part of the larger circle = <math>\frac {30^\circ}{360^\circ}(R^2\pi - r^2\pi) = \frac {1}{12}(2400\pi - 1200\pi) = 100\pi</math>. Hence the answer is <math>\boxed{314}</math>.
  
 
== See also ==
 
== See also ==
Line 20: Line 20:
  
 
[[Category:Intermediate Geometry Problems]]
 
[[Category:Intermediate Geometry Problems]]
 +
{{MAA Notice}}

Latest revision as of 15:42, 20 July 2021

Problem

A transformation of the first quadrant of the coordinate plane maps each point $(x,y)$ to the point $(\sqrt{x},\sqrt{y}).$ The vertices of quadrilateral $ABCD$ are $A=(900,300), B=(1800,600), C=(600,1800),$ and $D=(300,900).$ Let $k_{}$ be the area of the region enclosed by the image of quadrilateral $ABCD.$ Find the greatest integer that does not exceed $k_{}.$

Solution

\begin{eqnarray*}A' = & (\sqrt {900}, \sqrt {300})\\ B' = & (\sqrt {1800}, \sqrt {600})\\ C' = & (\sqrt {600}, \sqrt {1800})\\ D' = & (\sqrt {300}, \sqrt {900}) \end{eqnarray*}

First we see that lines passing through $AB$ and $CD$ have equations $y = \frac {1}{3}x$ and $y = 3x$, respectively. Looking at the points above, we see the equations for $A'B'$ and $C'D'$ are $y^2 = \frac {1}{3}x^2$ and $y^2 = 3x^2$, or, after manipulation $y = \frac {x}{\sqrt {3}}$ and $y = \sqrt {3}x$, respectively, which are still linear functions. Basically the square of the image points gives back the original points and we could plug them back into the original equation to get the equation of the image lines.

Now take a look at $BC$ and $AD$, which have the equations $y = - x + 2400$ and $y = - x + 1200$. The image equations hence are $x^2 + y^2 = 2400$ and $x^2 + y^2 = 1200$, respectively, which are the equations for circles.

1999 AIME-6.png

To find the area between the circles (actually, parts of the circles), we need to figure out the angle of the arc. This could be done by $\arctan \sqrt {3} - \arctan \frac {1}{\sqrt {3}} = 60^\circ - 30^\circ = 30^\circ$. So the requested areas are the area of the enclosed part of the smaller circle subtracted from the area enclosed by the part of the larger circle = $\frac {30^\circ}{360^\circ}(R^2\pi - r^2\pi) = \frac {1}{12}(2400\pi - 1200\pi) = 100\pi$. Hence the answer is $\boxed{314}$.

See also

1999 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 5 		Followed by
Problem 7
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1999_AIME_Problems/Problem_6&oldid=158794"