Difference between revisions of "2018 AMC 10A Problems/Problem 10"
Isabelchen (talk | contribs) (→Solution 8 (Analytic Geometry)) |
Isabelchen (talk | contribs) (→Solution 8 (Analytic Geometry)) |
||
| Line 92: | Line 92: | ||
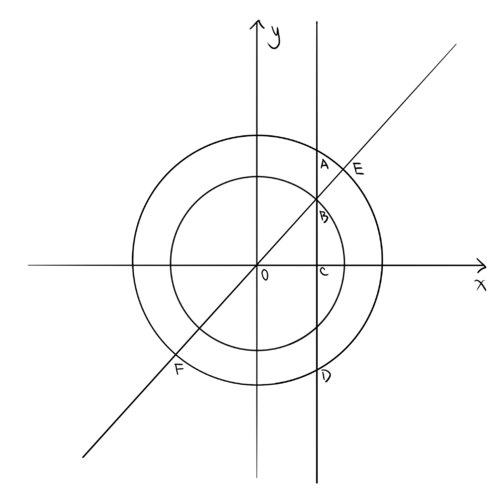
[[File:2018 AMC10 A P10.PNG|500px]] | [[File:2018 AMC10 A P10.PNG|500px]] | ||
| − | The problem can be represented by the above diagram. The large circle with center <math>O</math> has a radius of 7, the small circle with center <math>O</math> has a radius of 5. <math>AC=\sqrt{49-x^2}</math>, <math>BC=\sqrt{25-x^2}</math>, <math>AB=\sqrt{49-x^2} - \sqrt{25-x^2} = 3</math>, <math>BD=\sqrt{49-x^2} + \sqrt{25-x^2}</math>. | + | The problem can be represented by the above diagram. The large circle with center <math>O</math> has a radius of 7, the small circle with center <math>O</math> has a radius of 5. Point <math>C</math>'s X coordinate is <math>x</math>. <math>AC=CD=\sqrt{49-x^2}</math>, <math>BC=\sqrt{25-x^2}</math>, <math>AB=AC-BC=\sqrt{49-x^2} - \sqrt{25-x^2} = 3</math>, <math>BD=CD+BC=\sqrt{49-x^2} + \sqrt{25-x^2}</math>. |
| − | |||
| − | |||
| − | |||
| + | By Power of a Point, <math>AB \cdot BD=BE \cdot BF=(7-5) \cdot (7+5)=24</math>, <math>BD=\boxed{\textbf{(A) } 8}</math> | ||
~isabelchen | ~isabelchen | ||
Revision as of 01:02, 23 October 2021
Contents
Problem
Suppose that real number ![]() satisfies
satisfies ![]() What is the value of
What is the value of ![]() ?
?
![]()
Solutions
Solution 1
In order to eliminate the square roots, we multiply by the conjugate. Its value is the solution. The ![]() terms cancel nicely.
terms cancel nicely. ![]()
Given that ![]() . - cookiemonster2004
. - cookiemonster2004
Solution 2
Let ![]() , and let
, and let ![]() . Then
. Then ![]() . Substituting, we get
. Substituting, we get ![]() . Rearranging, we get
. Rearranging, we get ![]() . Squaring both sides and solving, we get
. Squaring both sides and solving, we get ![]() and
and ![]() . Adding, we get that the answer is
. Adding, we get that the answer is ![]() .
.
Solution 3
Put the equations to one side. ![]() can be changed into
can be changed into ![]() .
.
We can square both sides, getting us ![]()
That simplifies out to ![]() Dividing both sides by
Dividing both sides by ![]() gets us
gets us ![]() .
.
Following that, we can square both sides again, resulting in the equation ![]() . Simplifying that, we get
. Simplifying that, we get ![]() .
.
Substituting into the equation ![]() , we get
, we get ![]() . Immediately, we simplify into
. Immediately, we simplify into ![]() . The two numbers inside the square roots are simplified to be
. The two numbers inside the square roots are simplified to be ![]() and
and ![]() , so you add them up:
, so you add them up: ![]() .
.
~kevinmathz
Solution 4 (Geometric Interpretation)
Draw a right triangle ![]() with a hypotenuse
with a hypotenuse ![]() of length
of length ![]() and leg
and leg ![]() of length
of length ![]() . Draw
. Draw ![]() on
on ![]() such that
such that ![]() . Note that
. Note that ![]() and
and ![]() . Thus, from the given equation,
. Thus, from the given equation, ![]() . Using Law of Cosines on triangle
. Using Law of Cosines on triangle ![]() , we see that
, we see that ![]() so
so ![]() . Since
. Since ![]() is a
is a ![]() triangle,
triangle, ![]() and
and ![]() . Finally,
. Finally, ![]() .
.
![[asy] var s = sqrt(3); pair A = (-5*s/2, 0); pair B = (0,0); pair C = (0,5.5); pair D = (0,2.5); draw(A--B--C--A--D); rightanglemark(A, B, D); label("A", A, SW); label("B", B, SE); label("C", C, NE); label("D", D, E); label("7", (-5*s/4, 5.5/2), NW); label("120$^\circ$", D, NW); label("60$^\circ$", (0,2), SW); label("$x$", 0.5*A, S); draw(rightanglemark(A, B, C)); draw(anglemark(A, D, B)); markscalefactor = 0.04; draw(anglemark(C, D, A)); label("$\frac{5}{2}$", (0,1.25), E); label("3", (0,4), E); label("5", (-5*s/4, 5/4), N); [/asy]](http://latex.artofproblemsolving.com/d/c/9/dc946b3a968ec8ce149bcc5678a7513bfd6798f1.png)
Solution 5 (No Square Roots, Fastest)
We notice that the two expressions are conjugates, and therefore we can write them in a "difference-of-squares" format.
Namely, we can write it as ![]() . Given the
. Given the ![]() in the problem, we can divide
in the problem, we can divide ![]() .
.
-aze.10
Solution 6 (Symmetric Substitution)
Since ![]() , let
, let ![]() . Then we have
. Then we have ![]() . Squaring both sides gives us
. Squaring both sides gives us ![]() . Isolating the term with the square root, and squaring again, we get
. Isolating the term with the square root, and squaring again, we get ![]() . Then
. Then ![]() .
.
Solution 7 (Difference of Squares)
Let ![]() and
and ![]() . Then by difference of squares:
. Then by difference of squares:
![]() .
.
We can simplify this expression to get our answer. ![]() and from the given statement,
and from the given statement, ![]() . Now we have:
. Now we have:
![]() .
.
Hence, ![]() so our answer is
so our answer is ![]() .
.
~BakedPotato66
Solution 8 (Analytic Geometry)
The problem can be represented by the above diagram. The large circle with center ![]() has a radius of 7, the small circle with center
has a radius of 7, the small circle with center ![]() has a radius of 5. Point
has a radius of 5. Point ![]() 's X coordinate is
's X coordinate is ![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
By Power of a Point, ![]() ,
, ![]()
~isabelchen
Video Solutions
Video Solution 1
https://youtu.be/ba6w1OhXqOQ?t=1403
~ pi_is_3.14
Video Solution 2
https://youtu.be/zQG70XKAdeA ~ North America Math Contest Go Go Go
Video Solution 3
Video Solution 4
~savannahsolver
See Also
| 2018 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||