2018 AMC 10A Problems/Problem 24
- The following problem is from both the 2018 AMC 10A #24 and 2018 AMC 12A #18, so both problems redirect to this page.
Contents
[hide]Problem
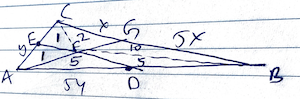
Triangle ![]() with
with ![]() and
and ![]() has area
has area ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() , and let
, and let ![]() be the midpoint of
be the midpoint of ![]() . The angle bisector of
. The angle bisector of ![]() intersects
intersects ![]() and
and ![]() at
at ![]() and
and ![]() , respectively. What is the area of quadrilateral
, respectively. What is the area of quadrilateral ![]() ?
?
![]()
Diagram
Solution 1
Let ![]() ,
, ![]() ,
, ![]() , and the length of the perpendicular from
, and the length of the perpendicular from ![]() through
through ![]() be
be ![]() . By angle bisector theorem, we have that
. By angle bisector theorem, we have that ![]() where
where ![]() . Therefore substituting we have that
. Therefore substituting we have that ![]() . By similar triangles, we have that
. By similar triangles, we have that ![]() , and the height of this trapezoid is
, and the height of this trapezoid is ![]() . Then, we have that
. Then, we have that ![]() . We wish to compute
. We wish to compute ![]() , and we have that it is
, and we have that it is ![]() by substituting.
by substituting.
Solution 2
For this problem, we have ![]() because of SAS and
because of SAS and ![]() . Therefore,
. Therefore, ![]() is a quarter of the area of
is a quarter of the area of ![]() , which is
, which is ![]() . Subsequently, we can compute the area of quadrilateral
. Subsequently, we can compute the area of quadrilateral ![]() to be
to be ![]() . Using the angle bisector theorem in the same fashion as the previous problem, we get that
. Using the angle bisector theorem in the same fashion as the previous problem, we get that ![]() is
is ![]() times the length of
times the length of ![]() . We want the larger piece, as described by the problem. Because the heights are identical, one area is
. We want the larger piece, as described by the problem. Because the heights are identical, one area is ![]() times the other, and
times the other, and ![]() .
.
Solution 3
The ratio of the ![]() to
to ![]() is
is ![]() by the Angle Bisector Theorem, so area of
by the Angle Bisector Theorem, so area of ![]() to the area of
to the area of ![]() is also
is also ![]() (They have the same height). Therefore, the area of
(They have the same height). Therefore, the area of ![]() is
is ![]() . Since
. Since ![]() is the midsegment of
is the midsegment of ![]() , so
, so ![]() is the midsegment of
is the midsegment of ![]() . Thus, the ratio of the area of
. Thus, the ratio of the area of ![]() to the area of
to the area of ![]() is
is ![]() , so the area of
, so the area of ![]() is
is ![]() . Therefore, the area of quadrilateral
. Therefore, the area of quadrilateral ![]() is
is ![]()
Solution 4
The area of quadrilateral ![]() is the area of
is the area of ![]() minus the area of
minus the area of ![]() . Notice,
. Notice, ![]() , so
, so ![]() , and since
, and since ![]() , the area of
, the area of ![]() . Given that the area of
. Given that the area of ![]() is
is ![]() , using
, using ![]() on side
on side ![]() yields
yields ![]() . Using the Angle Bisector Theorem,
. Using the Angle Bisector Theorem, ![]() , so the height of
, so the height of ![]() . Therefore our answer is
. Therefore our answer is ![]()
Solution 5 (Trigonometry)
We try to find the area of quadrilateral ![]() by subtracting the area outside the quadrilateral but inside triangle
by subtracting the area outside the quadrilateral but inside triangle ![]() . Note that the area of
. Note that the area of ![]() is equal to
is equal to ![]() and the area of triangle
and the area of triangle ![]() is equal to
is equal to ![]() . The ratio
. The ratio ![]() is thus equal to
is thus equal to ![]() and the area of triangle
and the area of triangle ![]() is
is ![]() . Let side
. Let side ![]() be equal to
be equal to ![]() , then
, then ![]() by the angle bisector theorem. Similarly, we find the area of triangle
by the angle bisector theorem. Similarly, we find the area of triangle ![]() to be
to be ![]() and the area of triangle
and the area of triangle ![]() to be
to be ![]() . A ratio between these two triangles yields
. A ratio between these two triangles yields ![]() , so
, so ![]() . Now we just need to find the area of triangle
. Now we just need to find the area of triangle ![]() and subtract it from the combined areas of
and subtract it from the combined areas of ![]() and
and ![]() , since we count it twice. Note that the angle bisector theorem also applies for
, since we count it twice. Note that the angle bisector theorem also applies for ![]() and
and ![]() , so thus
, so thus ![]() and we find
and we find ![]() , and the area outside
, and the area outside ![]() must be
must be ![]() , and we finally find
, and we finally find ![]() , and we are done.
, and we are done.
=
Solution 7 (Barycentrics)
Let our reference triangle be ![]() . Consequently, we have
. Consequently, we have ![]() ,
, ![]() ,
, ![]() Since
Since ![]() is the midpoint of
is the midpoint of ![]() , we have that
, we have that ![]() . Similarly, we have
. Similarly, we have ![]() Hence, the line through
Hence, the line through ![]() and
and ![]() is given by the equation
is given by the equation
![\[0 = \begin{vmatrix} x & y & z\\ 1 & 1 & 0\\ 1 & 0 & 1 \end{vmatrix}\]](http://latex.artofproblemsolving.com/e/d/8/ed8deb5b9df0401d259677c45a69a2c086e610e6.png)
Additionally, since all points on ![]() are characterized by
are characterized by ![]() , we may plug in for
, we may plug in for ![]() to get
to get ![]() . Thus, we have
. Thus, we have ![]() Now, we homogenize the coordinates for
Now, we homogenize the coordinates for ![]() to get
to get ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Splitting ![]() into
into ![]() we may now evaluate the two determinants:
we may now evaluate the two determinants:
![\[\begin{vmatrix} \frac{1}{2} & \frac{1}{2} & 0\\ 0 & 1 & 0\\ 0 & \frac{1}{6} & \frac{5}{6} \end{vmatrix}\]](http://latex.artofproblemsolving.com/e/c/0/ec0c77b483e5ac7a5beb342289fe926a855b0119.png)
![\[\begin{vmatrix} \frac{1}{2} & \frac{1}{12} & \frac{5}{12}\\ \frac{1}{2} & \frac{1}{2} & 0\\ 0 & \frac{5}{6} & \frac{1}{6} \end{vmatrix}.\]](http://latex.artofproblemsolving.com/b/3/d/b3dbffcc650f09bd9581fd8a89ac2a6d06755ffd.png)
After simplification, we get ![]() and
and ![]() , respectively. Summing, we get
, respectively. Summing, we get ![]() Hence,
Hence, ![]()
![]() Math0323
Math0323
Solution 8
We want to find ratios. Start off letting [AEF]=1. Then we know [AEF]=[CEF]=1 since AE=CE and they share the same height. Then, also because AE is half of AC, we see that [AEF]=1/4 [ACG] so [ACG]=4.
But we also know [EFGC]=3/4 [ACG], so [EFGC]=3 and then [CFG]=2. If [CFG]=2, then note that [FGB] must be 2*5=10.
Now, we see that [AFD]=5[AED] because EF=1/5 FD (from angle bisector theorem) and they share the same height. Then, because AD=DB, we have [FDB]=[FAD]=5.
Adding these up, we see that the ratio of [BGFD] to [ABC] is 15/24=5/8. 5/8*120 yields our answer of 75. ~mathboy282
Solution 9
Draw a nice diagram. Lets find some some areas. We will start by finding ![]() . The side length ratio of
. The side length ratio of ![]() to
to ![]() is
is ![]() , so the area ratio is
, so the area ratio is ![]() , so
, so ![]() . Lets look for information we have used yet. We still havent used the fact that
. Lets look for information we have used yet. We still havent used the fact that ![]() is an angle bisector. This hints at us using the angle bisector theorem. Letting
is an angle bisector. This hints at us using the angle bisector theorem. Letting ![]() , we have
, we have ![]() , and letting
, and letting ![]() ,
, ![]() . Now, we have
. Now, we have![]() . Doing the same thing with triangles
. Doing the same thing with triangles ![]() and
and ![]() , we find that
, we find that ![]() , and so
, and so ![]()
-jb2015007
Video Solution by Richard Rusczyk
https://artofproblemsolving.com/videos/amc/2018amc10a/469
~ dolphin7
Video Solution by OmegaLearn
https://youtu.be/4_x1sgcQCp4?t=4898
~ pi_is_3.14
See Also
| 2018 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 23 |
Followed by Problem 25 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2018 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 17 |
Followed by Problem 19 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()