Difference between revisions of "1995 AIME Problems"
| Line 1: | Line 1: | ||
== Problem 1 == | == Problem 1 == | ||
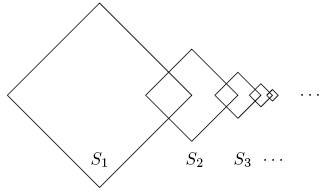
Square <math>\displaystyle S_{1}</math> is <math>1\times 1.</math> For <math>i\ge 1,</math> the lengths of the sides of square <math>\displaystyle S_{i+1}</math> are half the lengths of the sides of square <math>\displaystyle S_{i},</math> two adjacent sides of square <math>\displaystyle S_{i}</math> are perpendicular bisectors of two adjacent sides of square <math>\displaystyle S_{i+1},</math> and the other two sides of square <math>\displaystyle S_{i+1},</math> are the perpendicular bisectors of two adjacent sides of square <math>\displaystyle S_{i+2}.</math> The total area enclosed by at least one of <math>\displaystyle S_{1}, S_{2}, S_{3}, S_{4}, S_{5}</math> can be written in the form <math>\displaystyle m/n,</math> where <math>\displaystyle m</math> and <math>\displaystyle n</math> are relatively prime positive integers. Find <math>\displaystyle m-n.</math> | Square <math>\displaystyle S_{1}</math> is <math>1\times 1.</math> For <math>i\ge 1,</math> the lengths of the sides of square <math>\displaystyle S_{i+1}</math> are half the lengths of the sides of square <math>\displaystyle S_{i},</math> two adjacent sides of square <math>\displaystyle S_{i}</math> are perpendicular bisectors of two adjacent sides of square <math>\displaystyle S_{i+1},</math> and the other two sides of square <math>\displaystyle S_{i+1},</math> are the perpendicular bisectors of two adjacent sides of square <math>\displaystyle S_{i+2}.</math> The total area enclosed by at least one of <math>\displaystyle S_{1}, S_{2}, S_{3}, S_{4}, S_{5}</math> can be written in the form <math>\displaystyle m/n,</math> where <math>\displaystyle m</math> and <math>\displaystyle n</math> are relatively prime positive integers. Find <math>\displaystyle m-n.</math> | ||
| + | |||
| + | [[Image:AIME 1995 Problem 1.png]] | ||
[[1995 AIME Problems/Problem 1|Solution]] | [[1995 AIME Problems/Problem 1|Solution]] | ||
Revision as of 21:49, 21 January 2007
Contents
Problem 1
Square ![]() is
is ![]() For
For ![]() the lengths of the sides of square
the lengths of the sides of square ![]() are half the lengths of the sides of square
are half the lengths of the sides of square ![]() two adjacent sides of square
two adjacent sides of square ![]() are perpendicular bisectors of two adjacent sides of square
are perpendicular bisectors of two adjacent sides of square ![]() and the other two sides of square
and the other two sides of square ![]() are the perpendicular bisectors of two adjacent sides of square
are the perpendicular bisectors of two adjacent sides of square ![]() The total area enclosed by at least one of
The total area enclosed by at least one of ![]() can be written in the form
can be written in the form ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()