AoPS Academy
and 
Prove that
Let and 
Prove that
be complex numbers satisfying 
. Show that there exist some among the 
complex numbers such that the modulus of the sum of these complex numbers is not less than 
.
and 
be three positive integers. Prove that there exist a positive integer 
and a set of 
positive integers 
, such that, for every 
, the 
-ary expansion of is a 
-digit palindrome, and the 
-ary expansion is exactly 
.
, s.t :
, and square 
. Point 
and 
are on the circle, and 
is tangent to the circle at point 
. Let 
represent the midpoint of 
and 
represent the intersection between and circle. Prove that 
.
be a prime number. Define the set![\[
M_q = \left\{ x \in \mathbb{Z}^* \,\middle|\, \sqrt{x^2 + 2q^{2025} x} \in \mathbb{Q} \right\}.
\]](http://latex.artofproblemsolving.com/9/8/b/98b266a869cf5686cea86be51152ef234486993e.png)
.
be positive real number satisfy that: 
.Find the minimum: 
, holds 
with 
, holds 
and 
and let 
be the foot of perp from 
to 
. Clearly 
and 
by cyclic quads so done.
hope you all enjoyed it. The shortest solution I know is:
across 
intersects at , and define similarly. Then 
, so 
. But also since and are reflections across 
, 
and hence 
. So 
is the perpendicular bisector of 
.
and 
respectively be the reflections of about and 
and 
which gives us 
which combined with the above fact gives us that is the perpendicular bisector of 
which implies it is perpendicular to 
and 
be where the reflections hit . As 
, it suffices to show the midpoint of 
is the intouch point. But as 
and 
be reflection, this is clearly true say by coordinates or anything to keep track of lengths really.
meet 
at and meet at . Also, let 
and 
meet at 
and 
, respectively. Note that
and similarly 
, so 
is isosceles. But from the reflections we find that 
bisects 
and 
bisects 
, so is the incenter of . Thus bisects 
, which is enough to imply 
. is actually the 
-Excenter oops but it should be similar
over intersect at and let the reflection of over intersect at . Note that 
. Therefore, 
is isosceles, so it suffices to show that the foot from to , which we call , is the midpoint of 
.
. Therefore, by the Pythagorean Theorem or congruent triangles or something, we are done.
, 
to be the intersection of the perpendicular line to through with and . Let 
be the intersection with the perpendicular line to through with the reflection of about . We can easily prove 
and 
are congruent. If 
and 
are defined similarly, we see 
, thus 
, hence done.
hope you all enjoyed it. The shortest solution I know is: across intersects at , and define similarly. Then , so . But also since and are reflections across , and hence . So is the perpendicular bisector of .
be the contact triangle. Use complex numbers wrt the incircle, so the reflection of 
is the tangent at 
and similarly the reflection of 
is the tangent at 
. Thus 
and 
so 
collinear; done.
be the intersection of the angle bisector of 
with ; let be the intersection of the angle bisector of 
with ; let 
be the reflection of over the angle bisector of ; let 
be the reflection of over the angle bisector of . lies on line 
such that 
. Furthermore, line 
is the perpendicular bisector of 
. So, by symmetry, 
. Similarly, 
, so 
is isosceles. Lastly, since lies on the perpendicular bisectors of 
and 
, it also lies on the perpendicular bisector of 
, so it follows that 
as desired.
and respectively be the reflections of about and . Let 
is isosceles. Now by standard length calculations we can find that 
is bisects . We are done
and 
. Let and be the reflections of and 
over 
and 
, respectively. Notice that 
is the orthocenter of 
. Pappus on 
gives , 
, and collinear, which finishes.
denote the incircle and be it's tangent at . By reflection properties, we have 
. Thus, if we let 
intersect at 
then is the excircle of 
which implies is tangent to . Similarly, 
is tangent to . Thus, by Brianchon's on 
we have , 
, and 
concur. But, this point of concurrence is . Thus, 
are collinear which implies the result.
are reflected to 
and 
are reflected to 
.
are 
respectively. The condition implies 
where 
. Let 
. Similar reason yields 
. Now, the question is equivalent to prove 
.
. Since 
is the reflection of about , must intersect on , denote the intersection as . We have 
.
, we know an isosceles triangle's height, angle bisector, and median to the base are the same line, we get 
are collinear which yields 
as desired.
be a triangle with incenter . Suppose the reflection of across and the reflection of across intersect at a point . Prove that is perpendicular to . be the tengency points of the incercly.
.
lie on the same circle the symmetry of thiw circle with respect to is the circle 
.
we get that 
are collinear.SIlilary we have 
.
means that 
is the angel bisector of 
but also is the circumcenter of so 
witch givesw that 
it is enougt to prove that 
perpendicular to 
.
is tengent to the incircle.
and 
respectively. Let and intersect at and respectively. Let the incirle touch at . Using angle chasing 
. Use the fact that 
and 
to show that 
. Now it follows that , , and are collinear proving the claim.
across be 
, and the reflection of across be 
. Since we have reflected, 
and similarly 
. So, and both lie on . Also, 
and 
so is isosceles, implying that the incentre and orthocentre are collinear. Since is the reflection of across , 
and similarly 
, so and bisect and respectively, which means is the incentre of . So, 
and we are done.
be a triangle with incenter . Suppose the reflection of across and the reflection of across intersect at a point . Prove that is perpendicular to ., , be points of tangency of 
with , 
, , respectively
, 
be refelections of , across , respectively, are points of tangency of with tangents from to 
, are perpendicular bisecter of segments 
, 
respectively, so 
is an isosceles triangle at , 
and 
and denote the reflections of across lines and respectively. Further let and be the reflections of across and across . We can first locate all of these points. and lie on and points and lie on and respectively. be the intersection of line with side . Then, let 
denote the intersection of the reflection of side across . Note that, 
and 
which since 
is a common side implies that 
. Thus, 
which implies that 
is the reflection of across and 
as desired.
due to reflections so lies on the perpendicular bisector of segment . Further,![\[\measuredangle XA_BA_C = \measuredangle DA_BA_C = \measuredangle CAB = \measuredangle EAB = \measuredangle BA_CE = \measuredangle BA_CX\]](http://latex.artofproblemsolving.com/8/4/a/84a7c4c1da23c82234419d1fb7d9ac684ab42cba.png)
so 
is isosceles and in particular, lies on the perpendicular bisector of segment . Thus, 
is the perpendicular bisector of segment which implies as we wished to show.
. Let 
and 
be the reflections of across and respectively. It is evident that, 
because and are angle bisectors of 
and 
respectively.
. After some trivial angle chasing we get that the points 
and 
are concyclic. Also since, and are the reflections of across and respectively, we have 
i.e, is the center of 
.. Again angle chase to show that, 
and, 
.
. Let 
,
and replace 
with 
. Then, 
and 
. Now, 
.
and also, 
.
with 
.
. By "
Lemma" conclude that, 
and 
. We had thus, as desired. 
(
)
is isosceles
is cyclic
be real numbers so that 
and 
Show that
![\[ \frac{(10^4+324)(22^4+324)(34^4+324)(46^4+324)(58^4+324)}{(4^4+324)(16^4+324)(28^4+324)(40^4+324)(52^4+324)}. \]](http://latex.artofproblemsolving.com/c/f/0/cf007b7ce24aa95493617d1f4011e451e7c49126.png)
.
?
be the reflections of 
be the reflections of 
and 
,
so 
and since 
and 
are cyclic, 
so 
.
be the reflection of 
be the reflection of 
,
Using similar logic, we can deduce that 
and 
The reflection of line 
for 
.
,
for 
.
,
,
and since 
,
Therefore, we have that 
and 
Note that we must have 
so 
so 
Thus, we have that
By symmetry, it follows that 
Therefore, we have that 
Now, note that 
,
.![\begin{align*}
\begin{vmatrix} 0 & s-c & s-b \\ a & b & c \\ a^2(a-b-c) & b(a^2+bc-c^2-ab) & c(a^2+bc-b^2-ca) \end{vmatrix} &= -(s-c)[ac(a^2+bc - b^2-ca) - a^2c(a-b-c)] + (s-b)[ab(a^2+bc-c^2-ab) - a^2b(a-b-c)] \\ &= -(s-c)(ac)(a^2+bc-b^2-ca-a^2+ab+ac) + (s-b)(ab)(a^2+bc-c^2-ab-a^2+ab+ac) \\ &= -(s-c)(ac)(-b^2+ab+bc) + (s-b)(ab)(bc-c^2+ac) \\ &= -(s-c)(abc)(a+c-b) + (s-b)(abc)(a+b-c) \\ &= -(s-c)(abc)(2(s-b)) + (s-b)(abc)(2(s-c)) \\ &= 0,
\end{align*}](http://latex.artofproblemsolving.com/b/5/d/b5dc984119d4d5342de4d4f87405a67c00dedcaf.png)
so 
and 
.
and 
are tangent to 
(because of the symmetry) and notice that this implies that 
and the incenter leads to 
,
Let 
be the reflections of 
over 
Pappus on 
which finishes.
is the desired intersection point, then 
,
from 
and 
with 
on 
and 
,
![\[\angle XKC = \angle XLB = \angle A, \quad d(I, XK) = d(I, AB) = d(I, AC) = d(I, XL),\]](http://latex.artofproblemsolving.com/5/1/3/51356bd189971ca378b4572e6216b39837b085bd.png)
is isosceles and 
and 
.![\[\measuredangle IA_2B=\measuredangle BAI=\measuredangle IAD=\measuredangle DA_2I\]](http://latex.artofproblemsolving.com/f/9/e/f9e2177b065ed47ec9aba6adf79102dcde409e97.png)
and similarly 
bisects 
.
so 
be the reflections 
inversion at 
goes to 
.
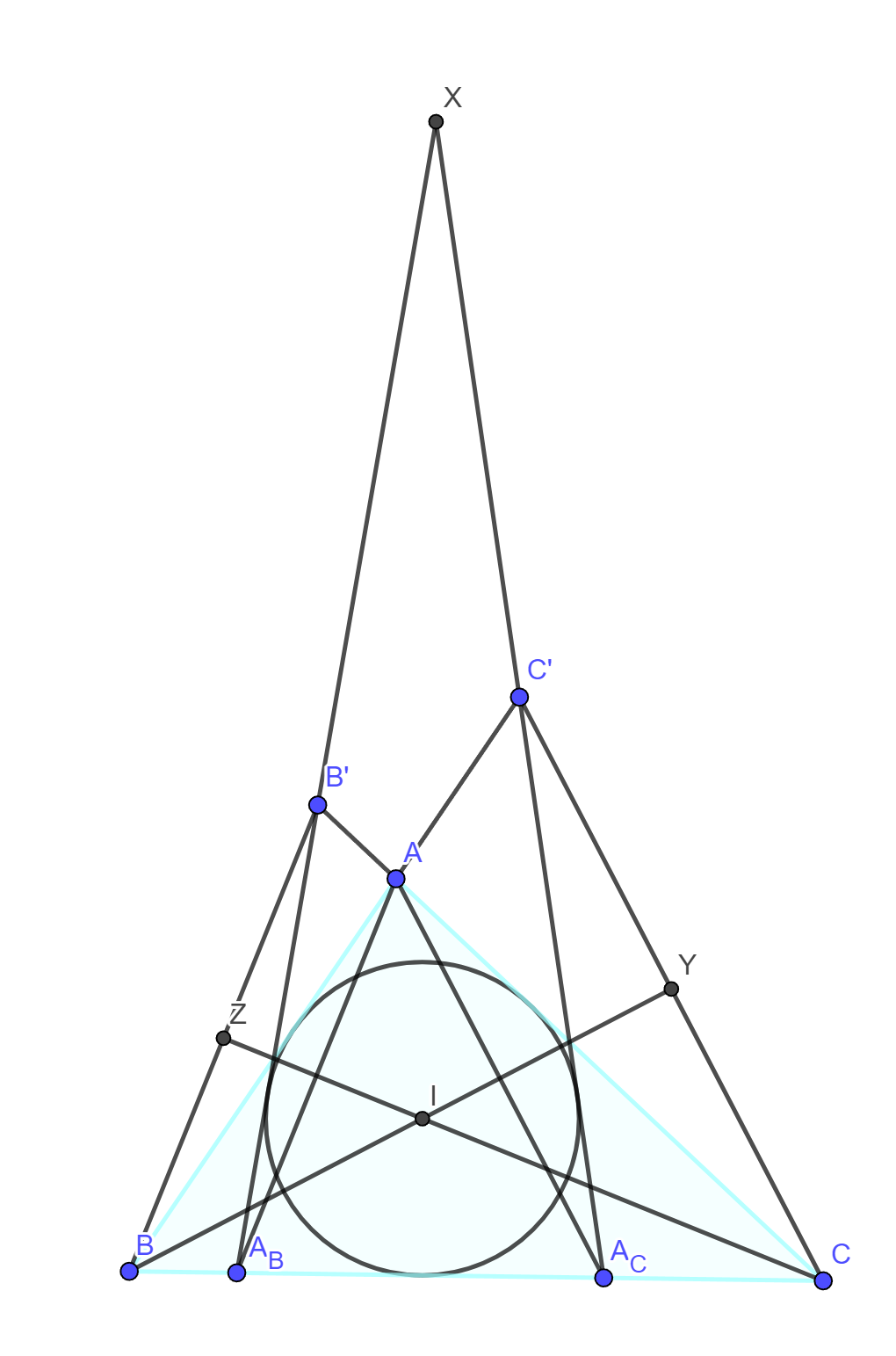
with 
.
with 
.
.
.
.
is the 
and 
,
.