Y by doxuanlong15052000, john111111, anantmudgal09, Davi-8191, AlastorMoody, Vietjung, rashah76, itslumi, v4913, tenebrine, sotpidot, HWenslawski, innout, anonman, megarnie, HamstPan38825, Jc426, Lamboreghini, CyclicISLscelesTrapezoid, tiendung2006, mathmax12, Adventure10, Mango247, geobo, Rounak_iitr
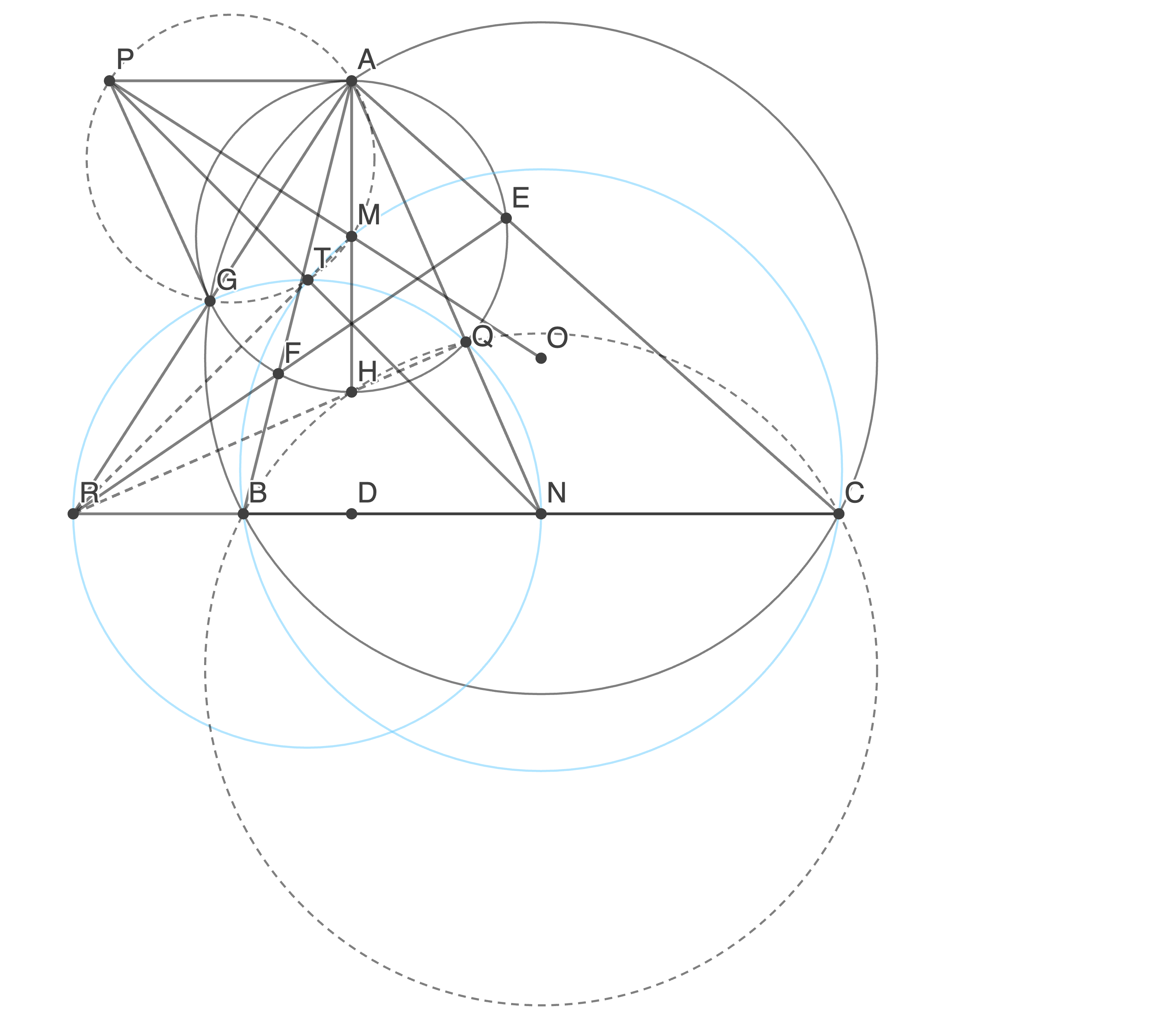
Let  be a scalene triangle with orthocenter
be a scalene triangle with orthocenter  and circumcenter
and circumcenter  . Denote by
. Denote by  ,
,  the midpoints of
the midpoints of  ,
,  . Suppose the circle
. Suppose the circle  with diameter
with diameter  meets the circumcircle of
meets the circumcircle of  at
at  , and meets line
, and meets line  at a point
at a point  . The tangent to
. The tangent to  at
at  meets line
meets line  at
at  . Show that the circumcircles of
. Show that the circumcircles of  and
and  intersect at a point
intersect at a point  on
on  .
.
Proposed by Evan Chen
Proposed by Evan Chen






![[asy]
unitsize(3.5cm);
pointpen=black; pathpen=rgb(0.4,0.6,0.8);
pointfontpen=fontsize(10);
path carc(pair A, pair B, pair C, real d=0, bool dir=CW) {
pair O=circumcenter(A,B,C);
return arc(O,circumradius(A,B,C),degrees(A-O)+d,degrees(C-O)-d,dir);
}
pair A=dir(120), B=dir(205), C=dir(-25), E=foot(B,C,A), F=foot(C,A,B), H=A+B+C, O=(0,0), M=(A+H)/2, N=(B+C)/2, R=extension(E,F,B,C), G=foot(N,A,R), P=extension(O,M,A,A+C-B), Q=extension(R,H,A,N), T=foot(M,P,N);
D(unitcircle,heavygreen);
DPA(CP(M,A)^^A--P--G,red);
D(carc(R,Q,N),purple);
D(carc(B,M,C),orange);
D(A--B--C--cycle,1);
DPA(A--R--E^^B--R--M^^P--N);
DPA(H--A--N^^P--O,dashed+pathpen);
D("A",A,dir(A));
D("B",B,SW);
D("C",C,SE);
D("E",E,dir(0));
D("F",F,dir(F));
D("G",G,NW);
D("H",H);
D("M",M,NE);
D("N",N);
D("O",O);
D("P",P,dir(P));
D("Q",Q);
D("R",R,dir(R));
D("T",T);
[/asy]](http://latex.artofproblemsolving.com/8/8/6/8864b85506c82fd5ae83bdc82dc71dee8c508cbf.png)



![[asy]
/* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki go to User:Azjps/geogebra */
import graph; size(14cm);
real labelscalefactor = 0.5; /* changes label-to-point distance */
pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */
pen dotstyle = black; /* point style */
real xmin = -16.617033912263082, xmax = 11.593068386334542, ymin = -9.011548785275052, ymax = 10.880190015018119; /* image dimensions */
pen wrwrwr = rgb(0.3803921568627451,0.3803921568627451,0.3803921568627451); pen wvvxds = rgb(0.396078431372549,0.3411764705882353,0.8235294117647058); pen dtsfsf = rgb(0.8274509803921568,0.1843137254901961,0.1843137254901961); pen sexdts = rgb(0.1803921568627451,0.49019607843137253,0.19607843137254902); pen qqttzz = rgb(0,0.2,0.6);
/* draw figures */
draw(circle((-2.9174386747164305,3.354763152375008), 3.337913182442299), linewidth(1.2) + wrwrwr);
draw(circle((-0.038467974241690905,1.1823987169809487), 6.212803014912631), linewidth(0.8) + wrwrwr);
draw((-2.9082937414146226,6.692663807534921)--(-9.565115715315315,-2.1294265880206846), linewidth(1.2) + wrwrwr);
draw(circle((-6.241277195015871,0.6126682821771595), 4.308942652924465), linewidth(1.2) + wvvxds);
draw((-7.357213737917736,6.704852629443152)--(-6.124706133324791,2.430047054064858), linewidth(0.8) + wrwrwr);
draw((-7.357213737917736,6.704852629443152)--(-2.9082937414146226,6.692663807534921), linewidth(1.2) + wrwrwr);
draw((-2.9082937414146226,6.692663807534921)--(-5.287560502057399,-2.1411459173720764), linewidth(1.2) + wrwrwr);
draw((-2.9082937414146226,6.692663807534921)--(5.192334686970401,-2.1698579589858515), linewidth(1.2) + wrwrwr);
draw(circle((-0.04483910939972965,-1.1430656157032155), 5.336880351816947), linewidth(0.8) + linetype("4 4") + wrwrwr);
draw(circle((-4.806364311429404,-2.1424642630998245), 4.758769263681267), linewidth(1.2) + linetype("4 4") + wrwrwr);
draw((-7.357213737917736,6.704852629443152)--(-0.047612907543499006,-2.155501938178964), linewidth(2) + linetype("2 2") + dtsfsf);
draw((-2.917438674716431,3.3547631523750088)--(-5.287560502057399,-2.1411459173720764), linewidth(1.2) + wrwrwr);
draw((-2.917438674716431,3.3547631523750088)--(5.192334686970401,-2.1698579589858515), linewidth(1.2) + wrwrwr);
draw((-4.585955856235141,0.46379189196806214)--(0.4078416776100351,3.0646338847137744), linewidth(1.6) + sexdts);
draw((-2.917438674716431,3.3547631523750088)--(-2.93251363705325,-2.1475981005638687), linewidth(1.6) + sexdts);
draw(circle((-2.9202124728602006,2.3423268298992608), 1.012440122192103), linewidth(1.2) + qqttzz);
draw((-2.917438674716431,3.3547631523750088)--(-0.047612907543499006,-2.155501938178964), linewidth(0.8) + dotted + wrwrwr);
draw((-4.585955856235141,0.46379189196806214)--(-0.047612907543499006,-2.155501938178964), linewidth(1.2) + linetype("2 2") + wrwrwr);
draw((-0.047612907543499006,-2.155501938178964)--(0.4078416776100351,3.0646338847137744), linewidth(1.2) + linetype("2 2") + wrwrwr);
draw((-2.9082937414146226,6.692663807534921)--(-0.047612907543499006,-2.155501938178964), linewidth(0.8) + wrwrwr);
draw((-9.565115715315315,-2.1294265880206846)--(5.192334686970401,-2.1698579589858515), linewidth(1.2) + wrwrwr);
draw((-2.9082937414146226,6.692663807534921)--(-2.917438674716431,3.3547631523750088), linewidth(1.6) + sexdts);
draw((-4.516499937369707,4.56135543079989)--(-2.917438674716431,3.3547631523750088), linewidth(1.2) + wrwrwr);
/* dots and labels */
dot((-2.9082937414146226,6.692663807534921),linewidth(2pt) + dotstyle);
label("$A$", (-2.7832337466046315,6.8114252604126975), NE * labelscalefactor);
dot((-5.287560502057399,-2.1411459173720764),linewidth(3pt) + dotstyle);
label("$B$", (-5.164214603003363,-1.9590232106256544), NE * labelscalefactor);
dot((5.192334686970401,-2.1698579589858515),linewidth(3pt) + dotstyle);
label("$C$", (5.324156764423958,-1.9891622088079168), NE * labelscalefactor);
dot((0.4078416776100351,3.0646338847137744),linewidth(2pt) + dotstyle);
label("$E$", (0.5320560534442341,3.194745478541212), NE * labelscalefactor);
dot((-4.585955856235141,0.46379189196806214),linewidth(2pt) + dotstyle);
label("$F$", (-4.471017644811327,0.5726526366843854), NE * labelscalefactor);
dot((-2.93251363705325,-2.1475981005638687),linewidth(2pt) + dotstyle);
label("$S$", (-2.813372744786894,-2.0193012069901792), NE * labelscalefactor);
dot((-2.926583608018239,0.016862497215096122),linewidth(2pt) + dotstyle);
label("$H$", (-2.813372744786894,0.15070666213271208), NE * labelscalefactor);
dot((-9.565115715315315,-2.1294265880206846),linewidth(2pt) + dotstyle);
label("$R$", (-9.443952344884625,-2.0193012069901792), NE * labelscalefactor);
dot((-6.124706133324791,2.430047054064858),linewidth(2pt) + dotstyle);
label("$G$", (-6.00810655210671,2.5618265167137024), NE * labelscalefactor);
dot((-0.047612907543499006,-2.155501938178964),linewidth(2pt) + dotstyle);
label("$N$", (0.07997108071029789,-2.0494402051724414), NE * labelscalefactor);
dot((-2.917438674716431,3.3547631523750088),linewidth(2pt) + dotstyle);
label("$M$", (-2.7832337466046315,3.465996462181574), NE * labelscalefactor);
dot((-7.357213737917736,6.704852629443152),linewidth(2pt) + dotstyle);
label("$P$", (-7.243805477579469,6.8114252604126975), NE * labelscalefactor);
dot((-0.9559422750255506,0.6539861738886703),linewidth(2pt) + dotstyle);
label("$Q$", (-0.8241988647575746,0.7836256239602221), NE * labelscalefactor);
dot((-4.516499937369707,4.56135543079989),linewidth(2pt) + dotstyle);
label("$Y$", (-4.410739648446802,4.671556389472069), NE * labelscalefactor);
dot((-2.089057089312553,1.7642128883409183),linewidth(2pt) + dotstyle);
label("$I$", (-1.9694807956835465,1.89876855670393), NE * labelscalefactor);
dot((-3.914722019191468,2.5320259687490156),linewidth(2pt) + dotstyle);
label("$T'$", (-3.807959684801554,2.6522435112604894), NE * labelscalefactor);
dot((-2.92298627100397,1.3298905074235121),linewidth(2pt) + dotstyle);
label("$X$", (-2.813372744786894,1.4466835839699943), NE * labelscalefactor);
clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle);
/* end of picture */
[/asy]](http://latex.artofproblemsolving.com/5/b/2/5b2ee02ca0861cd74cc76892c8c2062b0b768680.png)






