Difference between revisions of "2021 AMC 12A Problems/Problem 17"
m |
(→Solution 7 (Triogeometry)) |
||
| (80 intermediate revisions by 22 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{duplicate|[[2021 AMC 10A Problems | + | {{duplicate|[[2021 AMC 10A Problems/Problem 17|2021 AMC 10A #17]] and [[2021 AMC 12A Problems/Problem 17|2021 AMC 12A #17]]}} |
==Problem== | ==Problem== | ||
| Line 6: | Line 6: | ||
<math>\textbf{(A) }65 \qquad \textbf{(B) }132 \qquad \textbf{(C) }157 \qquad \textbf{(D) }194\qquad \textbf{(E) }215</math> | <math>\textbf{(A) }65 \qquad \textbf{(B) }132 \qquad \textbf{(C) }157 \qquad \textbf{(D) }194\qquad \textbf{(E) }215</math> | ||
| − | == Solution 1 == | + | ==Diagram== |
| + | <asy> | ||
| + | /* Made by MRENTHUSIASM */ | ||
| + | size(300); | ||
| + | pair A, B, C, D, O, P; | ||
| + | C = (43,0); | ||
| + | D = (0,0); | ||
| + | B = intersectionpoints(Circle(C,43),Circle(D,66))[0]; | ||
| + | A = intersectionpoints(Circle(D,4*sqrt(190)),B--B+100*dir(180))[1]; | ||
| + | P = midpoint(B--D); | ||
| + | O = intersectionpoint(A--C,B--D); | ||
| + | dot("$C$",C,1.5*SE,linewidth(4)); | ||
| + | dot("$D$",D,1.5*SW,linewidth(4)); | ||
| + | dot("$B$",B,1.5*NE,linewidth(4)); | ||
| + | dot("$A$",A,1.5*NW,linewidth(4)); | ||
| + | dot("$P$",P,1.5*N,linewidth(4)); | ||
| + | dot("$O$",O,1.5*S,linewidth(4)); | ||
| + | markscalefactor=0.25; | ||
| + | draw(rightanglemark(A,D,O),red); | ||
| + | draw(A--B--C--D--cycle^^A--C^^B--D^^C--P); | ||
| + | label("$43$",B--C,E); | ||
| + | label("$43$",C--D,S); | ||
| + | label("$11$",midpoint(O--P),NW); | ||
| + | </asy> | ||
| + | ~MRENTHUSIASM | ||
| + | |||
| + | == Solution 1 (Similar Triangles and Pythagorean Theorem) == | ||
| + | Angle chasing* reveals that <math>\triangle BPC\sim\triangle BDA</math>, therefore | ||
| + | <cmath>2=\frac{BD}{BP}=\frac{AB}{BC}=\frac{AB}{43},</cmath> | ||
| + | or <math>AB=86</math>. | ||
| + | |||
| + | Additional angle chasing shows that <math>\triangle ABO\sim\triangle CDO</math>, therefore | ||
| + | <cmath>2=\frac{AB}{CD}=\frac{BO}{OD}=\frac{BP+11}{BP-11},</cmath> | ||
| + | or <math>BP=33</math> and <math>BD=66</math>. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Since <math>\triangle ADB</math> is right, the Pythagorean theorem implies that | Since <math>\triangle ADB</math> is right, the Pythagorean theorem implies that | ||
| − | <cmath>AD=\sqrt{86^2-66^2} | + | <cmath>AD=\sqrt{86^2-66^2}=4\sqrt{190}.</cmath> |
| − | + | The answer is <math>4+190=\boxed{\textbf{(D) }194}</math>. | |
| − | <math> | + | |
| + | * Angle Chasing: If we set <math>\angle DBC = \alpha</math>, then we know that <math>\angle DCB = 180^\circ-2\alpha</math> because <math>\triangle DBC</math> is isosceles. Then, <math>\angle BCP = 90^\circ-\alpha</math>, so <math>\angle BPC</math> is a right angle. Because <math>\angle BDC = \alpha</math> and <math>\overline{AB}\parallel\overline{DC}</math>, we conclude that <math>\angle ABD = \alpha</math> too. Lastly, because <math>\triangle BPC</math> and <math>\triangle BDA</math> are both right triangles, they are similar by AA. | ||
| + | |||
| + | ~mn28407 (Solution) | ||
| − | ~ | + | ~mm (Angle Chasing Remark) |
| − | + | ~eagleye ~MRENTHUSIASM ~charyyu83 (Minor Edits) | |
| − | |||
| − | Since <math>\triangle | + | ==Solution 2 (Similar Triangles, Areas, Pythagorean Theorem)== |
| + | Since <math>\triangle BCD</math> is isosceles with base <math>\overline{BD},</math> it follows that median <math>\overline{CP}</math> is also an altitude. Let <math>OD=x</math> and <math>CP=h,</math> so <math>PB=x+11.</math> | ||
| − | Let the brackets denote areas. Notice that <math>[ | + | Since <math>\angle AOD=\angle COP</math> by vertical angles, we conclude that <math>\triangle AOD\sim\triangle COP</math> by AA, from which <math>\frac{AD}{CP}=\frac{OD}{OP},</math> or <cmath>AD=CP\cdot\frac{OD}{OP}=h\cdot\frac{x}{11}.</cmath> Let the brackets denote areas. Notice that <math>[AOD]=[BOC]</math> (By the same base and height, we deduce that <math>[ACD]=[BDC].</math> Subtracting <math>[OCD]</math> from both sides gives <math>[AOD]=[BOC].</math>). Doubling both sides produces |
<cmath>\begin{align*} | <cmath>\begin{align*} | ||
| − | 2[ | + | 2[AOD]&=2[BOC] \ |
| − | \frac{ | + | OD\cdot AD&=OB\cdot CP \ |
| − | x^2&= | + | x\left(\frac{hx}{11}\right)&=(x+22)h \ |
| − | (x | + | x^2&=11(x+22). |
| − | |||
\end{align*}</cmath> | \end{align*}</cmath> | ||
| + | Rearranging and factoring result in <math>(x-22)(x+11)=0,</math> from which <math>x=22.</math> | ||
| − | + | Applying the Pythagorean Theorem to right <math>\triangle CPB,</math> we have <cmath>h=\sqrt{43^2-33^2}=\sqrt{(43+33)(43-33)}=\sqrt{760}=2\sqrt{190}.</cmath> Finally, we get <cmath>AD=h\cdot\frac{x}{11}=4\sqrt{190},</cmath> so the answer is <math>4+190=\boxed{\textbf{(D) }194}.</math> | |
~MRENTHUSIASM | ~MRENTHUSIASM | ||
| − | == Video Solution (Using Similar Triangles, Pythagorean Theorem) == | + | ==Solution 3 (Short)== |
| + | Let <math>CP = y</math>. <math>CP</math> a is perpendicular bisector of <math>DB.</math> Then, let <math>DO = x,</math> thus <math>DP = PB = 11+x.</math> | ||
| + | |||
| + | (1) <math>\triangle CPO \sim \triangle ADO,</math> so we get <math>\frac{AD}{x} = \frac{y}{11},</math> or <math>AD = \frac{xy}{11}.</math> | ||
| + | |||
| + | (2) Applying Pythagorean Theorem on <math>\triangle CDP</math> gives <math>(11+x)^2 + y^2 = 43^2.</math> | ||
| + | |||
| + | (3) <math>\triangle BPC \sim \triangle BDA</math> with ratio <math>1:2,</math> so <math>AD = 2y</math> using the fact that <math>P</math> is the midpoint of <math>BD</math>. | ||
| + | |||
| + | Thus, <math>\frac{xy}{11} = 2y,</math> or <math>x = 22.</math> And <math>y = \sqrt{43^2 - 33^2} = 2 \sqrt{190},</math> so <math>AD = 4 \sqrt{190}</math> and the answer is <math>4+190=\boxed{\textbf{(D) }194}.</math> | ||
| + | |||
| + | ~ ccx09 | ||
| + | |||
| + | ==Solution 4 (Extending the Line)== | ||
| + | Observe that <math>\triangle BPC</math> is congruent to <math>\triangle DPC</math>; both are similar to <math>\triangle BDA</math>. Let's extend <math>\overline{AD}</math> and <math>\overline{BC}</math> past points <math>D</math> and <math>C</math> respectively, such that they intersect at a point <math>E</math>. Observe that <math>\angle BDE</math> is <math>90</math> degrees, and that <math>\angle DBE \cong \angle PBC \cong \angle DBA \implies \angle DBE \cong \angle DBA</math>. Thus, by ASA, we know that <math>\triangle ABD \cong \triangle EBD</math>, thus, <math>AD = ED</math>, meaning <math>D</math> is the midpoint of <math>AE</math>. | ||
| + | Let <math>M</math> be the midpoint of <math>\overline{DE}</math>. Note that <math>\triangle CME</math> is congruent to <math>\triangle BPC</math>, thus <math>BC = CE</math>, meaning <math>C</math> is the midpoint of <math>\overline{BE}.</math> | ||
| + | |||
| + | Therefore, <math>\overline{AC}</math> and <math>\overline{BD}</math> are both medians of <math>\triangle ABE</math>. This means that <math>O</math> is the centroid of <math>\triangle ABE</math>; therefore, because the centroid divides the median in a 2:1 ratio, <math>\frac{BO}{2} = DO = \frac{BD}{3}</math>. Recall that <math>P</math> is the midpoint of <math>BD</math>; <math>DP = \frac{BD}{2}</math>. The question tells us that <math>OP = 11</math>; <math>DP-DO=11</math>; we can write this in terms of <math>DB</math>; <math>\frac{DB}{2}-\frac{DB}{3} = \frac{DB}{6} = 11 \implies DB = 66</math>. | ||
| + | |||
| + | We are almost finished. Each side length of <math>\triangle ABD</math> is twice as long as the corresponding side length <math>\triangle CBP</math> or <math>\triangle CPD</math>, since those triangles are similar; this means that <math>AB = 2 \cdot 43 = 86</math>. Now, by Pythagorean theorem on <math>\triangle ABD</math>, <math>AB^{2} - BD^{2} = AD^{2} \implies 86^{2}-66^{2} = AD^{2} \implies AD = \sqrt{3040} \implies AD = 4 \sqrt{190}</math>. | ||
| + | |||
| + | The answer is <math>4+190 = \boxed{\textbf{(D) }194}</math>. | ||
| + | |||
| + | ~ihatemath123 | ||
| + | |||
| + | ==Solution 5== | ||
| + | Since <math>P</math> is the midpoint of isosceles triangle <math>BCD</math>, it would be pretty easy to see that <math>CP\perp BD</math>. Since <math>AD\perp BD</math> as well, <math>AD\parallel CP</math>. Connecting <math>AP</math>, it’s obvious that <math>[ADC]=[ADP]</math>. Since <math>DP=BP</math>, <math>[APB]=[ADC]</math>. | ||
| + | |||
| + | Since <math>P</math> is the midpoint of <math>BD</math>, the height of <math>\triangle APB</math> on side <math>AB</math> is half that of <math>\triangle ADC</math> on <math>CD</math>. Since <math>[APB]=[ADC]</math>, <math>AB=2CD</math>. | ||
| + | |||
| + | As a basic property of a trapezoid, <math>\triangle AOB \sim \triangle COD</math>, so <math>\frac{OB}{OD}=\frac{AB}{CD}=2</math>, or <math>OB=2OD</math>. Letting <math>OD=x</math>, then <math>PB=DP=11+x</math>, and <math>OB=22+x</math>. Hence <math>22+x=2x</math> and <math>x=22</math>. | ||
| + | |||
| + | Since <math>\triangle AOD \sim \triangle COP</math>, <math>\frac{AD}{PC}=\frac{OD}{OP}=2</math>. Since <math>PD=11+22=33</math>, <math>PC=\sqrt{43^2-33^2}=\sqrt{760}</math>. | ||
| + | |||
| + | So, <math>AD=2\sqrt{760}=4\sqrt{190}</math>. The correct answer is <math>\boxed{\textbf{(D) }194}</math>. | ||
| + | |||
| + | ==Solution 6 (Coordinate Geometry) == | ||
| + | |||
| + | Let <math>D</math> be the origin of the cartesian coordinate plane, <math>B</math> lie on the positive <math>x</math>-axis, and <math>A</math> lie on the negative <math>y</math>-axis. Then let the coordinates of <math>B = (2a,0), A = (0, -2b).</math> Then the slope of <math>AB</math> is <math>\frac{b}{a}.</math> Since <math>AB \parallel CD</math> the slope of <math>CD</math> is the same. Note that as <math>\triangle DCB</math> is isosceles <math>C</math> lies on <math>x = a.</math> Thus since <math>CD</math> has equation <math>y = \frac{b}{a}x</math> (<math>D</math> is the origin), <math>C = (a,b).</math> Therefore <math>AC</math> has equation <math>y = \frac{3b}{a}x - 2b</math> and intersects <math>BD</math> (<math>x</math>-axis) at <math>O =\left(\frac{2}{3}a, 0\right).</math> The midpoint of <math>BD</math> is <math>P = (a,0),</math> so <math>OP = \frac{a}{3} = 11,</math> from which <math>a = 33.</math> Then by Pythagorean theorem on <math>\triangle DPC</math> (<math>\triangle DBC</math> is isosceles), we have <math>b = \sqrt{43^2 - 33^2} = 2\sqrt{190},</math> so <math>2b=4\sqrt{190}.</math> | ||
| + | |||
| + | Finally, the answer is <math>4+190=\boxed{\textbf{(D) }194}.</math> | ||
| + | |||
| + | ~Aaryabhatta1 | ||
| + | |||
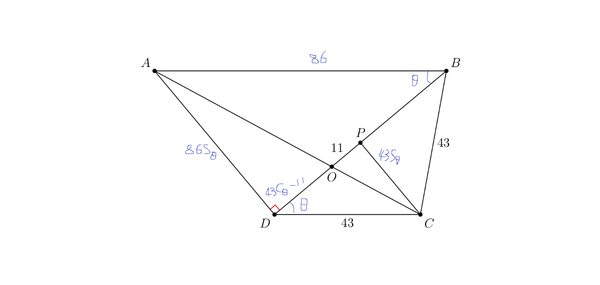
| + | ==Solution 7 (Trigonometry) == | ||
| + | |||
| + | [[Image:2021_12A_p17.png|thumb|center|600px|]] | ||
| + | |||
| + | set <math>\angle BDC = \theta </math> | ||
| + | |||
| + | BD = 2*DP = 2*43*Cos(<math>\theta</math>) | ||
| + | |||
| + | AB = BD / Cos(<math>\angle DBA</math>) = BD / Cos(<math>\theta</math>) = 2 *43 * Cos(<math>\theta</math>) / Cos(<math>\theta</math>) = 86 | ||
| + | |||
| + | OP/DO = CP / AD | ||
| + | |||
| + | 11 / (43Cos(<math>\theta</math>) - 11) = 43Sin(<math>\theta</math>) / 86 Sin(<math>\theta</math>) | ||
| + | |||
| + | Cos(<math>\theta</math>) = 33/ 43 | ||
| + | |||
| + | AD = 86 * Sin(<math>\theta</math>) = 2<math>\sqrt{760}= 4\sqrt{190}=\boxed{\textbf{(D) }194}</math>. | ||
| + | |||
| + | ~[https://artofproblemsolving.com/wiki/index.php/User:Cyantist luckuso] | ||
| + | |||
| + | == Video Solution by OmegaLearn (Using Similar Triangles, Pythagorean Theorem) == | ||
https://youtu.be/gjeSGJy_ld4 | https://youtu.be/gjeSGJy_ld4 | ||
~ pi_is_3.14 | ~ pi_is_3.14 | ||
| + | |||
| + | ==Video Solution by Punxsutawney Phil== | ||
| + | https://youtube.com/watch?v=rtdovluzgQs | ||
| + | |||
| + | == Video Solution by Mathematical Dexterity == | ||
| + | https://www.youtube.com/watch?v=QzAVdsgBBqg | ||
==See also== | ==See also== | ||
Latest revision as of 22:51, 23 July 2024
- The following problem is from both the 2021 AMC 10A #17 and 2021 AMC 12A #17, so both problems redirect to this page.
Contents
[hide]- 1 Problem
- 2 Diagram
- 3 Solution 1 (Similar Triangles and Pythagorean Theorem)
- 4 Solution 2 (Similar Triangles, Areas, Pythagorean Theorem)
- 5 Solution 3 (Short)
- 6 Solution 4 (Extending the Line)
- 7 Solution 5
- 8 Solution 6 (Coordinate Geometry)
- 9 Solution 7 (Trigonometry)
- 10 Video Solution by OmegaLearn (Using Similar Triangles, Pythagorean Theorem)
- 11 Video Solution by Punxsutawney Phil
- 12 Video Solution by Mathematical Dexterity
- 13 See also
Problem
Trapezoid ![]() has
has ![]() , and
, and ![]() . Let
. Let ![]() be the intersection of the diagonals
be the intersection of the diagonals ![]() and
and ![]() , and let
, and let ![]() be the midpoint of
be the midpoint of ![]() . Given that
. Given that ![]() , the length of
, the length of ![]() can be written in the form
can be written in the form ![]() , where
, where ![]() and
and ![]() are positive integers and
are positive integers and ![]() is not divisible by the square of any prime. What is
is not divisible by the square of any prime. What is ![]() ?
?
![]()
Diagram
![[asy] /* Made by MRENTHUSIASM */ size(300); pair A, B, C, D, O, P; C = (43,0); D = (0,0); B = intersectionpoints(Circle(C,43),Circle(D,66))[0]; A = intersectionpoints(Circle(D,4*sqrt(190)),B--B+100*dir(180))[1]; P = midpoint(B--D); O = intersectionpoint(A--C,B--D); dot("$C$",C,1.5*SE,linewidth(4)); dot("$D$",D,1.5*SW,linewidth(4)); dot("$B$",B,1.5*NE,linewidth(4)); dot("$A$",A,1.5*NW,linewidth(4)); dot("$P$",P,1.5*N,linewidth(4)); dot("$O$",O,1.5*S,linewidth(4)); markscalefactor=0.25; draw(rightanglemark(A,D,O),red); draw(A--B--C--D--cycle^^A--C^^B--D^^C--P); label("$43$",B--C,E); label("$43$",C--D,S); label("$11$",midpoint(O--P),NW); [/asy]](http://latex.artofproblemsolving.com/7/f/8/7f82402bf8ed8faa95eb3ffc36d6e380627bd1d3.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution 1 (Similar Triangles and Pythagorean Theorem)
Angle chasing* reveals that ![]() , therefore
, therefore
![]() or
or ![]() .
.
Additional angle chasing shows that ![]() , therefore
, therefore
![]() or
or ![]() and
and ![]() .
.
Since ![]() is right, the Pythagorean theorem implies that
is right, the Pythagorean theorem implies that
![]() The answer is
The answer is ![]() .
.
- Angle Chasing: If we set
 , then we know that
, then we know that  because
because  is isosceles. Then,
is isosceles. Then,  , so
, so  is a right angle. Because
is a right angle. Because  and
and  , we conclude that
, we conclude that  too. Lastly, because
too. Lastly, because  and
and  are both right triangles, they are similar by AA.
are both right triangles, they are similar by AA.
~mn28407 (Solution)
~mm (Angle Chasing Remark)
~eagleye ~MRENTHUSIASM ~charyyu83 (Minor Edits)
Solution 2 (Similar Triangles, Areas, Pythagorean Theorem)
Since ![]() is isosceles with base
is isosceles with base ![]() it follows that median
it follows that median ![]() is also an altitude. Let
is also an altitude. Let ![]() and
and ![]() so
so ![]()
Since ![]() by vertical angles, we conclude that
by vertical angles, we conclude that ![]() by AA, from which
by AA, from which ![]() or
or ![]() Let the brackets denote areas. Notice that
Let the brackets denote areas. Notice that ![]() (By the same base and height, we deduce that
(By the same base and height, we deduce that ![]() Subtracting
Subtracting ![]() from both sides gives
from both sides gives ![]() ). Doubling both sides produces
). Doubling both sides produces
![\begin{align*} 2[AOD]&=2[BOC] \\ OD\cdot AD&=OB\cdot CP \\ x\left(\frac{hx}{11}\right)&=(x+22)h \\ x^2&=11(x+22). \end{align*}](http://latex.artofproblemsolving.com/c/6/5/c6515ed23627aa952cb96807252e3f5d36ceb8bb.png) Rearranging and factoring result in
Rearranging and factoring result in ![]() from which
from which ![]()
Applying the Pythagorean Theorem to right ![]() we have
we have ![]() Finally, we get
Finally, we get ![]() so the answer is
so the answer is ![]()
~MRENTHUSIASM
Solution 3 (Short)
Let ![]() .
. ![]() a is perpendicular bisector of
a is perpendicular bisector of ![]() Then, let
Then, let ![]() thus
thus ![]()
(1) ![]() so we get
so we get ![]() or
or ![]()
(2) Applying Pythagorean Theorem on ![]() gives
gives ![]()
(3) ![]() with ratio
with ratio ![]() so
so ![]() using the fact that
using the fact that ![]() is the midpoint of
is the midpoint of ![]() .
.
Thus, ![]() or
or ![]() And
And ![]() so
so ![]() and the answer is
and the answer is ![]()
~ ccx09
Solution 4 (Extending the Line)
Observe that ![]() is congruent to
is congruent to ![]() ; both are similar to
; both are similar to ![]() . Let's extend
. Let's extend ![]() and
and ![]() past points
past points ![]() and
and ![]() respectively, such that they intersect at a point
respectively, such that they intersect at a point ![]() . Observe that
. Observe that ![]() is
is ![]() degrees, and that
degrees, and that ![]() . Thus, by ASA, we know that
. Thus, by ASA, we know that ![]() , thus,
, thus, ![]() , meaning
, meaning ![]() is the midpoint of
is the midpoint of ![]() .
Let
.
Let ![]() be the midpoint of
be the midpoint of ![]() . Note that
. Note that ![]() is congruent to
is congruent to ![]() , thus
, thus ![]() , meaning
, meaning ![]() is the midpoint of
is the midpoint of ![]()
Therefore, ![]() and
and ![]() are both medians of
are both medians of ![]() . This means that
. This means that ![]() is the centroid of
is the centroid of ![]() ; therefore, because the centroid divides the median in a 2:1 ratio,
; therefore, because the centroid divides the median in a 2:1 ratio, ![]() . Recall that
. Recall that ![]() is the midpoint of
is the midpoint of ![]() ;
; ![]() . The question tells us that
. The question tells us that ![]() ;
; ![]() ; we can write this in terms of
; we can write this in terms of ![]() ;
; ![]() .
.
We are almost finished. Each side length of ![]() is twice as long as the corresponding side length
is twice as long as the corresponding side length ![]() or
or ![]() , since those triangles are similar; this means that
, since those triangles are similar; this means that ![]() . Now, by Pythagorean theorem on
. Now, by Pythagorean theorem on ![]() ,
, ![]() .
.
The answer is ![]() .
.
~ihatemath123
Solution 5
Since ![]() is the midpoint of isosceles triangle
is the midpoint of isosceles triangle ![]() , it would be pretty easy to see that
, it would be pretty easy to see that ![]() . Since
. Since ![]() as well,
as well, ![]() . Connecting
. Connecting ![]() , it’s obvious that
, it’s obvious that ![]() . Since
. Since ![]() ,
, ![]() .
.
Since ![]() is the midpoint of
is the midpoint of ![]() , the height of
, the height of ![]() on side
on side ![]() is half that of
is half that of ![]() on
on ![]() . Since
. Since ![]() ,
, ![]() .
.
As a basic property of a trapezoid, ![]() , so
, so ![]() , or
, or ![]() . Letting
. Letting ![]() , then
, then ![]() , and
, and ![]() . Hence
. Hence ![]() and
and ![]() .
.
Since ![]() ,
, ![]() . Since
. Since ![]() ,
, ![]() .
.
So, ![]() . The correct answer is
. The correct answer is ![]() .
.
Solution 6 (Coordinate Geometry)
Let ![]() be the origin of the cartesian coordinate plane,
be the origin of the cartesian coordinate plane, ![]() lie on the positive
lie on the positive ![]() -axis, and
-axis, and ![]() lie on the negative
lie on the negative ![]() -axis. Then let the coordinates of
-axis. Then let the coordinates of ![]() Then the slope of
Then the slope of ![]() is
is ![]() Since
Since ![]() the slope of
the slope of ![]() is the same. Note that as
is the same. Note that as ![]() is isosceles
is isosceles ![]() lies on
lies on ![]() Thus since
Thus since ![]() has equation
has equation ![]() (
(![]() is the origin),
is the origin), ![]() Therefore
Therefore ![]() has equation
has equation ![]() and intersects
and intersects ![]() (
(![]() -axis) at
-axis) at ![]() The midpoint of
The midpoint of ![]() is
is ![]() so
so ![]() from which
from which ![]() Then by Pythagorean theorem on
Then by Pythagorean theorem on ![]() (
(![]() is isosceles), we have
is isosceles), we have ![]() so
so ![]()
Finally, the answer is ![]()
~Aaryabhatta1
Solution 7 (Trigonometry)
set ![]()
BD = 2*DP = 2*43*Cos(![]() )
)
AB = BD / Cos(![]() ) = BD / Cos(
) = BD / Cos(![]() ) = 2 *43 * Cos(
) = 2 *43 * Cos(![]() ) / Cos(
) / Cos(![]() ) = 86
) = 86
OP/DO = CP / AD
11 / (43Cos(![]() ) - 11) = 43Sin(
) - 11) = 43Sin(![]() ) / 86 Sin(
) / 86 Sin(![]() )
)
Cos(![]() ) = 33/ 43
) = 33/ 43
AD = 86 * Sin(![]() ) = 2
) = 2![]() .
.
Video Solution by OmegaLearn (Using Similar Triangles, Pythagorean Theorem)
~ pi_is_3.14
Video Solution by Punxsutawney Phil
https://youtube.com/watch?v=rtdovluzgQs
Video Solution by Mathematical Dexterity
https://www.youtube.com/watch?v=QzAVdsgBBqg
See also
| 2021 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 16 |
Followed by Problem 18 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2021 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 16 |
Followed by Problem 18 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()