Difference between revisions of "2010 AMC 12A Problems/Problem 8"
(→Solution 2) |
(→Solution 4) |
||
| (26 intermediate revisions by 13 users not shown) | |||
| Line 4: | Line 4: | ||
<math>\textbf{(A)}\ 60^\circ \qquad \textbf{(B)}\ 75^\circ \qquad \textbf{(C)}\ 90^\circ \qquad \textbf{(D)}\ 105^\circ \qquad \textbf{(E)}\ 120^\circ</math> | <math>\textbf{(A)}\ 60^\circ \qquad \textbf{(B)}\ 75^\circ \qquad \textbf{(C)}\ 90^\circ \qquad \textbf{(D)}\ 105^\circ \qquad \textbf{(E)}\ 120^\circ</math> | ||
| − | == Solution == | + | == Solution 1 == |
<center>[[File:AMC 2010 12A Problem 8.png]]</center> | <center>[[File:AMC 2010 12A Problem 8.png]]</center> | ||
| Line 16: | Line 16: | ||
\angle BAC &= \angle EAC + \angle BAE = 60^\circ - x + x = 60^\circ\end{align*}</cmath> | \angle BAC &= \angle EAC + \angle BAE = 60^\circ - x + x = 60^\circ\end{align*}</cmath> | ||
| − | Since <math>\frac{AC}{AB} = \frac{1}{2}</math>, triangle <math>ABC</math> is a <math>30-60-90</math> triangle, so <math>\angle BCA = \boxed{90^\circ\,\textbf{(C)}}</math>. | + | Since <math>\frac{AC}{AB} = \frac{1}{2}</math> and the angle between the hypotenuse and the shorter side is <math>60^\circ</math>, triangle <math>ABC</math> is a <math>30-60-90</math> triangle, so <math>\angle BCA = \boxed{90^\circ\,\textbf{(C)}}</math>. |
| + | == Solution 2(Trig and Angle Chasing) == | ||
| + | Let <cmath>AB=2a, AC=a</cmath> | ||
| + | Let <cmath>\angle BAE=\angle ACD=x</cmath> | ||
| + | Because <math>\triangle CFE</math> is equilateral, we get <math>\angle FCE=60</math>, so <math>\angle ACB=60+x</math> | ||
| − | = | + | Because <math>\triangle CFE</math> is equilateral, we get <math>\angle CFE=60</math>. |
| − | + | Angles <math>AFD</math> and <math>CFE</math> are vertical, so <math>\angle AFD=60</math>. | |
| − | <cmath>\frac{ | + | |
| + | By triangle <math>ADF</math>, we have <math>\angle ADF=120-x</math>, and because of line <math>AB</math>, we have <math>\angle BDC=60+x</math>. | ||
| + | |||
| + | Because Of line <math>BC</math>, we have <math>\angle AEB=120</math>, and by line <math>CD</math>, we have <math>\angle DFE=120</math>. | ||
| + | |||
| + | By quadrilateral <math>BDFE</math>, we have <math>\angle ABC=60-x</math>. | ||
| + | |||
| + | By the Law of Sines: | ||
| + | <cmath>\frac{\sin(60-x)}{a}=\frac{\sin(60+x)}{2a}\implies 2\sin(60-x)=\sin(60+x)</cmath> | ||
| + | |||
| + | By the sine addition formula(<math>\sin(a+b)=\sin(a)\cos(b)+\cos(a)\sin(b)</math>): | ||
| + | <cmath>2(\sin(60)\cos(-x)+\cos(60)\sin(-x))=\sin(60)\cos(x)+\cos(60)\sin(x)</cmath> | ||
| + | |||
| + | Because cosine is an even function, and sine is an odd function, we have <cmath>2\sin(60)\cos(x)-2\cos(60)\sin(x)=\sin(60)\cos(x)+\cos(60)\sin(x) \implies \sin(60)\cos(x)=3\cos(60)\sin(x)</cmath> | ||
| + | |||
| + | We know that <math>\sin(60)=\frac{\sqrt{3}}{2}</math>, and <math>\cos(60)=\frac{1}{2}</math>, hence | ||
| + | <cmath>\frac{\sqrt{3}}{2}\cos(x)=\frac{3}{2}\sin(x)\implies \tan(x)=\frac{\sqrt{3}}{3}</cmath> | ||
| + | |||
| + | The only value of <math>x</math> that satisfies <math>60+x<180</math>(because <math>60+x</math> is an angle of the triangle) is <math>x=30^{\circ}</math>. We seek to find <math>\angle ACB</math>, which as we found before is <math>60+x</math>, which is <math>90</math>. The answer is <math>90, \text{or} \textbf{(C)}</math> | ||
| + | |||
| + | -vsamc | ||
| + | |||
| + | == Solution 3 (Similar Triangles) == | ||
| + | Notice that <math>\angle AEB=\angle AFC = 120^{\circ}</math> and <math>\angle ACF=\angle BAE</math>. Hence, triangle AEB is similar to triangle CFA. Since <math>AB=2AC</math>, <math>AE=2CF=2FE</math>, as triangle CFE is equilateral. Therefore, <math>AF=FE=FC</math>, and since <math>\angle AFC=120^{\circ}</math>, <math>x=30</math>. Thus, the measure of <math>\angle ACE</math> equals to <math>\angle FCE+\angle ACF=90^{\circ}, \text{or} \textbf{(C)}</math> | ||
| + | -HarryW | ||
| + | |||
| + | |||
| + | == Solution 4 == | ||
| + | Notice that <math>\triangle ADF \sim \triangle CDA</math> (by AA Similarity.) Since the corresponding angles of a pair of similar triangles are congruent, we have <math>\angle DAC = \angle DFA = 60^\circ.</math> Since <math>AB = 2 \cdot AC</math> and <math>\angle DFA = 60^\circ,</math> we have that <math>\triangle ABC</math> is congruent by SAS to a <math>30-60-90</math> right triangle, which gives the answer <math>\boxed{\textbf{(C)}}</math>. | ||
| + | ~clever14710owl | ||
| + | |||
| + | ==Video Solution by the Beauty of Math== | ||
| + | https://youtu.be/kU70k1-ONgM?t=785 | ||
| + | |||
| + | == Video Solution by OmegaLearn == | ||
| + | https://youtu.be/O_o_-yjGrOU?t=58 | ||
| + | |||
| + | ~ pi_is_3.14 | ||
== See also == | == See also == | ||
| + | {{AMC10 box|year=2010|ab=A|num-b=13|num-a=15}} | ||
{{AMC12 box|year=2010|num-b=7|num-a=9|ab=A}} | {{AMC12 box|year=2010|num-b=7|num-a=9|ab=A}} | ||
[[Category:Introductory Geometry Problems]] | [[Category:Introductory Geometry Problems]] | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 19:33, 19 August 2024
Contents
Problem
Triangle ![]() has
has ![]() . Let
. Let ![]() and
and ![]() be on
be on ![]() and
and ![]() , respectively, such that
, respectively, such that ![]() . Let
. Let ![]() be the intersection of segments
be the intersection of segments ![]() and
and ![]() , and suppose that
, and suppose that ![]() is equilateral. What is
is equilateral. What is ![]() ?
?
![]()
Solution 1
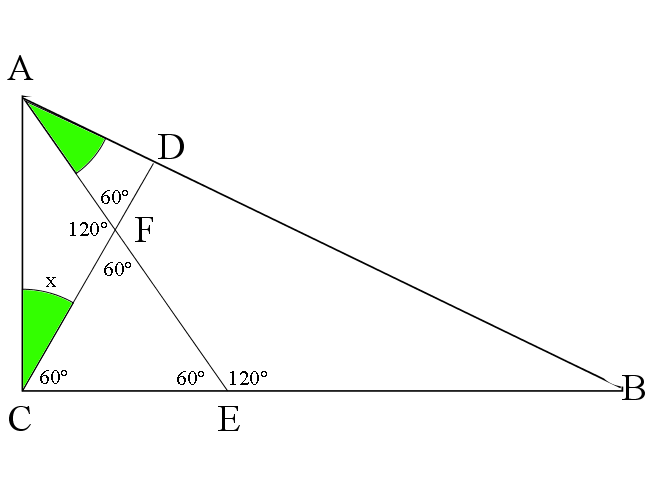
Let ![]() .
.

Since ![]() and the angle between the hypotenuse and the shorter side is
and the angle between the hypotenuse and the shorter side is ![]() , triangle
, triangle ![]() is a
is a ![]() triangle, so
triangle, so ![]() .
.
Solution 2(Trig and Angle Chasing)
Let ![]() Let
Let ![]() Because
Because ![]() is equilateral, we get
is equilateral, we get ![]() , so
, so ![]()
Because ![]() is equilateral, we get
is equilateral, we get ![]() .
.
Angles ![]() and
and ![]() are vertical, so
are vertical, so ![]() .
.
By triangle ![]() , we have
, we have ![]() , and because of line
, and because of line ![]() , we have
, we have ![]() .
.
Because Of line ![]() , we have
, we have ![]() , and by line
, and by line ![]() , we have
, we have ![]() .
.
By quadrilateral ![]() , we have
, we have ![]() .
.
By the Law of Sines:
![]()
By the sine addition formula(![]() ):
):
![]()
Because cosine is an even function, and sine is an odd function, we have ![]()
We know that ![]() , and
, and ![]() , hence
, hence
![]()
The only value of ![]() that satisfies
that satisfies ![]() (because
(because ![]() is an angle of the triangle) is
is an angle of the triangle) is ![]() . We seek to find
. We seek to find ![]() , which as we found before is
, which as we found before is ![]() , which is
, which is ![]() . The answer is
. The answer is ![]()
-vsamc
Solution 3 (Similar Triangles)
Notice that ![]() and
and ![]() . Hence, triangle AEB is similar to triangle CFA. Since
. Hence, triangle AEB is similar to triangle CFA. Since ![]() ,
, ![]() , as triangle CFE is equilateral. Therefore,
, as triangle CFE is equilateral. Therefore, ![]() , and since
, and since ![]() ,
, ![]() . Thus, the measure of
. Thus, the measure of ![]() equals to
equals to ![]() -HarryW
-HarryW
Solution 4
Notice that ![]() (by AA Similarity.) Since the corresponding angles of a pair of similar triangles are congruent, we have
(by AA Similarity.) Since the corresponding angles of a pair of similar triangles are congruent, we have ![]() Since
Since ![]() and
and ![]() we have that
we have that ![]() is congruent by SAS to a
is congruent by SAS to a ![]() right triangle, which gives the answer
right triangle, which gives the answer ![]() .
~clever14710owl
.
~clever14710owl
Video Solution by the Beauty of Math
https://youtu.be/kU70k1-ONgM?t=785
Video Solution by OmegaLearn
https://youtu.be/O_o_-yjGrOU?t=58
~ pi_is_3.14
See also
| 2010 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2010 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 7 |
Followed by Problem 9 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 









