Difference between revisions of "Euler line"
(→De Longchamps point of Euler line) |
(→See also) |
||
| (85 intermediate revisions by 2 users not shown) | |||
| Line 26: | Line 26: | ||
[[Image:Euler Line.PNG||500px|frame|center]] | [[Image:Euler Line.PNG||500px|frame|center]] | ||
| + | |||
| + | ==The points of intersection of the Euler line with the sides of the triangle== | ||
| + | <i><b>Acute triangle</b></i> | ||
| + | [[File:Euler line crosspoints.png|450px|right]] | ||
| + | Let <math>\triangle ABC</math> be the acute triangle where <math>AC > BC > AB.</math> | ||
| + | Denote <math>\angle A = \alpha, \angle B = \beta, \angle C = \gamma</math> | ||
| + | <cmath>\implies \beta > \alpha > \gamma.</cmath> | ||
| + | |||
| + | Let Euler line cross lines <math>AB, AC,</math> and <math>BC</math> in points <math>D, E,</math> and <math>F,</math> respectively. | ||
| + | |||
| + | Then point <math>D</math> lyes on segment <math>AB, \frac {\vec BD}{\vec DA} = n = \frac {\tan \alpha – \tan \gamma}{\tan \beta – \tan \gamma} > 0.</math> | ||
| + | |||
| + | Point <math>E</math> lyes on segment <math>AC, \frac {\vec AE}{\vec EC} = \frac {\tan \beta – \tan \gamma}{\tan \beta – \tan \alpha} > 0.</math> | ||
| + | |||
| + | Point <math>F</math> lyes on ray <math>BC, \frac {\vec {BF}}{\vec {CF}} = \frac {\tan \alpha – \tan \gamma}{\tan \beta – \tan \alpha} > 0.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Denote <math>n = \frac {\vec BD}{\vec DA}, m = \frac {\vec CE}{\vec EA}, p = \frac {\vec CX}{\vec XB}, X \in BC, q = \frac {AY}{YX}, Y \in AX.</math> | ||
| + | |||
| + | We use the formulae <math>m + pn = \frac {p+1}{q}</math> (see Claim “Segments crossing inside triangle” in “Schiffler point” in “Euler line”). | ||
| + | |||
| + | Centroid <math>G</math> lyes on median <math>AA'' \implies X = A'' , Y = G, p = 1, q = 2 \implies m+n=1.</math> | ||
| + | |||
| + | Orthocenter <math>H</math> lyes on altitude <math>AA' \implies X = A', Y = H, p = \frac {\vec {CX}}{\vec {XB}} = \frac {\tan \beta}{\tan \gamma}, q = \frac {AY}{YX}.</math> | ||
| + | <cmath>q = \frac {\vec {AH}}{\vec {HA'}} = \frac {\cos \alpha}{\cos \beta \cdot \cos \gamma} = \tan \beta \cdot \tan \gamma – 1 \implies</cmath> | ||
| + | <cmath>m \tan \gamma + n \tan \beta = \frac {\tan \beta + \tan \gamma}{1 – \tan \beta \cdot \tan \gamma} = – \tan \alpha.</cmath> | ||
| + | Therefore | ||
| + | <cmath>\frac {\vec {BD}}{\vec {DA}} = n = \frac {\tan \alpha – \tan \gamma}{\tan \beta – \tan \gamma} > 0,</cmath> | ||
| + | <cmath>\frac {\vec {CE}}{\vec {EA}} = m =\frac {\tan \beta – \tan \alpha}{\tan \beta – \tan \gamma} > 0.</cmath> | ||
| + | We use the signed version of Menelaus's theorem and get | ||
| + | <cmath>\frac {\vec {BF}}{\vec {FC}} = \frac {\tan \alpha – \tan \gamma}{ \tan \alpha –\tan \beta} < 0.</cmath> | ||
| + | |||
| + | <i><b>Obtuse triangle</b></i> | ||
| + | [[File:Euler line obtuse triangle.png|400px|right]] | ||
| + | Let <math>\triangle ABC</math> be the obtuse triangle where <math>BC > AC > AB \implies \alpha > \beta > \gamma.</math> | ||
| + | |||
| + | Let Euler line cross lines <math>AB, AC,</math> and <math>BC</math> in points <math>D, E,</math> and <math>F,</math> respectively. | ||
| + | |||
| + | Similarly we get <math>F \in BC, \frac {\vec {BF}}{\vec {FC}} = \frac {\tan \gamma – \tan \alpha}{ \tan \beta –\tan \alpha} > 0.</math> | ||
| + | |||
| + | <cmath>E \in AC, \frac {\vec {CE}}{\vec {EA}} = \frac {\tan \beta – \tan \alpha}{\tan \beta – \tan \gamma} > 0.</cmath> | ||
| + | <math>D \in</math> ray <math>BA, \frac {\vec {BD}}{\vec {AD}} = \frac {\tan \gamma – \tan \alpha}{\tan \beta – \tan \gamma} > 0.</math> | ||
| + | |||
| + | <i><b>Right triangle</b></i> | ||
| + | |||
| + | Let <math>\triangle ABC</math> be the right triangle where <math>\angle BAC = 90^\circ.</math> Then Euler line contain median from vertex <math>A.</math> | ||
| + | |||
| + | <i><b>Isosceles triangle</b></i> | ||
| + | |||
| + | Let <math>\triangle ABC</math> be the isosceles triangle where <math>AC = AB.</math> Then Euler line contain median from vertex <math>A.</math> | ||
| + | |||
| + | <i><b>Corollary: Euler line is parallel to side</b></i> | ||
| + | |||
| + | Euler line <math>DE</math> is parallel to side <math>BC</math> iff <math>\tan \beta \cdot \tan \gamma = 3.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | <math>DE||BC \implies \frac {BD}{DA} = \frac {\tan \alpha – \tan \gamma}{\tan \beta – \tan \gamma}= | ||
| + | \frac {CE}{EA} = \frac {\tan \beta – \tan \alpha}{\tan \beta – \tan \gamma}.</math> | ||
| + | |||
| + | After simplification in the case <math>\beta \ne \gamma</math> we get <math>2 \tan \alpha = \tan \beta + \tan \gamma.</math> | ||
| + | <cmath>180^\circ – \alpha = \beta + \gamma \implies \tan \alpha = \frac{\tan \beta + \tan \gamma}{\tan \beta \cdot \tan \gamma – 1} \implies \tan \beta \cdot \tan \gamma = 3.</cmath> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Angles between Euler line and the sides of the triangle== | ||
| + | [[File:Euler line side angle.png|450px|right]] | ||
| + | Let Euler line of the <math>\triangle ABC</math> cross lines <math>AB, AC,</math> and <math>BC</math> in points <math>D, E,</math> and <math>F,</math> respectively. | ||
| + | Denote <math>\angle A = \alpha, \angle B = \beta, \angle C = \gamma,</math> smaller angles between the Euler line and lines <math>BC, AC,</math> and <math>AB</math> as <math>\theta_A, \theta_B,</math> and <math>\theta_C,</math> respectively. | ||
| + | |||
| + | Prove that <math>\tan \theta_A = \vert \frac{3 – \tan \beta \cdot \tan \gamma}{\tan \beta – \tan \gamma} \vert,</math> | ||
| + | <cmath>\tan \theta_B = |\frac{3 – \tan \alpha \cdot \tan \gamma}{\tan \alpha – \tan \gamma}\vert, | ||
| + | \tan \theta_C = |\frac{3 – \tan \beta \cdot \tan \alpha}{\tan \beta – \tan \alpha}\vert.</cmath> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | WLOG, <math>AC > BC > AB \implies \frac {\vec {BF}}{\vec {CF}} = \frac {\tan \alpha – \tan \gamma}{\tan \beta – \tan \alpha} > 0.</math> | ||
| + | |||
| + | Let <math>|BC| = 2a, M</math> be the midpoint <math>BC, O</math> be the circumcenter of <math>\triangle ABC \implies OM = \frac {a}{\tan \alpha}.</math> | ||
| + | |||
| + | <cmath>MF = MC + CF, \frac {\vec {BF}}{\vec {CF}} = \frac {\vec {BC + CF}}{\vec {CF}} = \frac {2a}{|CF|}+ 1 =\frac {\tan \alpha – \tan \gamma}{\tan \beta – \tan \alpha} \implies</cmath> | ||
| + | <cmath>\frac {|MF|}{a} = \frac {\tan \beta – \tan \gamma}{2 \tan \alpha – \tan \beta – \tan \gamma} \implies</cmath> | ||
| + | <cmath>\tan \theta_A = \frac {|OM|}{|MF|} = |\frac {3 – \tan \beta \cdot \tan \gamma}{\tan \beta – \tan \gamma}|.</cmath> | ||
| + | |||
| + | Symilarly, for other angles. | ||
| + | |||
| + | *[[Gossard perspector]] | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Distances along Euler line== | ||
| + | [[File:OH distance.png|400px|right]] | ||
| + | Let <math>H, G, O,</math> and <math>R</math> be orthocenter, centroid, circumcenter, and circumradius of the <math>\triangle ABC,</math> respectively. | ||
| + | <cmath>a = BC, b = AC, c = AB,</cmath> | ||
| + | <cmath>\alpha = \angle A,\beta = \angle B,\gamma = \angle C.</cmath> | ||
| + | |||
| + | Prove that <math>HO^2 = R^2 (1 - 8 \cos A \cos B \cos C),</math> | ||
| + | <cmath>GO^2 = R^2 - \frac {a^2 + b^2 + c^2}{9}.</cmath> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | WLOG, <math>ABC</math> is an acute triangle, <math>\beta \ge \gamma.</math> | ||
| + | |||
| + | <cmath>OA = R, AH = 2 R \cos \alpha, \angle BAD = \angle OAC = 90^\circ - \beta \implies</cmath> | ||
| + | <cmath>\angle OAH = \alpha - 2\cdot (90^\circ - \beta) = \alpha + \beta + \gamma - 180^\circ + \beta - \gamma = \beta - \gamma .</cmath> | ||
| + | <cmath>HO^2 = AO^2 + AH^2 - 2 AH \cdot AO \cos \angle OAC = R^2 + (2 R \cos \alpha)^2 - 2 R \cdot 2R \cos \alpha \cdot \cos (\beta - \gamma).</cmath> | ||
| + | <cmath>\frac {HO^2}{R^2} = 1 + 4 \cos \alpha (\cos \alpha - \cos (\beta - \gamma) = 1 - 4 \cos \alpha (\cos (\beta + \gamma) + \cos (\beta – \gamma)) = 1 - 8 \cos \alpha \cos \beta \cos \gamma.</cmath> | ||
| + | <cmath>\frac {HO^2}{R^2} = 1 + 4 \cos^2 \alpha - 4 \cos \alpha \cos (\beta - \gamma) = 5 - 4 \sin^2 \alpha + 4 \cos (\beta + \gamma) \cos (\beta - \gamma)</cmath> | ||
| + | <cmath>HO^2 = 5R^2 - 4R^2 \sin^2 \alpha + 2R^2 \cos 2\beta + 2R^2 \cos 2 \gamma = 9R^2 - 4R^2 \sin^2 \alpha - 4R^2 \sin^2 \beta - 4 R^2\sin^2 \gamma</cmath> | ||
| + | <cmath>HO^2 = 9R^2 - a^2 - b^2 - c^2, GO^2 = \frac {HO^2}{9} = R^2 - \frac {a^2 + b^2 + c^2}{9}.</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Position of Kimberling centers on the Euler line== | ||
| + | [[File:Kimberling points on Euler line.png|450px|right]] | ||
| + | Let triangle ABC be given. Let <math>H = X(4), O = X(3), R</math> and <math>r</math> are orthocenter, circumcenter, circumradius and inradius, respectively. | ||
| + | |||
| + | We use point <math>\vec O = \vec X(3)</math> as origin and <math>\vec {HO}</math> as a unit vector. | ||
| + | |||
| + | We find Kimberling center X(I) on Euler line in the form of | ||
| + | <cmath>\vec X(I) = \vec O + k_i \cdot \vec {OH}.</cmath> | ||
| + | For a lot of Kimberling centers the coefficient <math>k_i</math> is a function of only two parameters <math>J = \frac {|OH|}{R}</math> and <math>t = \frac {r}{R}.</math> | ||
| + | |||
| + | Centroid <math>X(2)</math> | ||
| + | <cmath>X(2) = X(3) + \frac {1}{3} (X(4) - X(3)) \implies k_2 = \frac {1}{3}.</cmath> | ||
| + | Nine-point center <math>X(5)</math> | ||
| + | <cmath>X(5) = X(3) + \frac {1}{2} (X(4) - X(3)) \implies k_5 = \frac {1}{2}.</cmath> | ||
| + | de Longchamps point <math>X(20)</math> | ||
| + | <cmath>X(20) = X(3) - (X(4) - X(3)) \implies k_{20} = - 1.</cmath> | ||
| + | Schiffler point <math>X(21)</math> | ||
| + | <cmath>X(21) = X(3) + \frac {1}{3 + 2r/R} (X(4) + X(3)) \implies k_{21} = \frac {1}{3 + 2t}.</cmath> | ||
| + | Exeter point <math>X(22)</math> | ||
| + | <cmath>X(22) = X(3) + \frac {2}{J^2 - 3} (X(4) - X(3)) \implies k_{22} = \frac {2}{J^2 - 3}.</cmath> | ||
| + | Far-out point <math>X(23)</math> | ||
| + | <cmath>X(23) = X(3) + \frac {3}{J^2} (X(4) - X(3)) \implies k_{23} = \frac {3}{J^2}.</cmath> | ||
| + | Perspector of ABC and orthic-of-orthic triangle <math>X(24)</math> | ||
| + | <cmath>X(24) = X(3) + \frac {2}{J^2+1} (X(4) - X(3)) \implies k_{24} = \frac {2}{J^2 + 1}.</cmath> | ||
| + | Homothetic center of orthic and tangential triangles <math>X(25)</math> | ||
| + | <cmath>X(25) = X(3) + \frac {4}{J^2+3} (X(4) - X(3)) \implies k_{25} = \frac {4}{J^2 + 3}.</cmath> | ||
| + | Circumcenter of the tangential triangle <math>X(26)</math> | ||
| + | <cmath>X(26) = X(3) + \frac {2}{J^2 - 1}(X(4) - X(3)) \implies k_{26} = \frac {2}{J^2 - 1}.</cmath> | ||
| + | |||
| + | Midpoint of X(3) and <math>X(5)</math> | ||
| + | <cmath>X(140) = X(3) + \frac {1}{4} (X(4) - X(3)) \implies k_{140} = \frac {1}{4}.</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
==Triangles with angles of <math>60^\circ</math> or <math>120^\circ</math>== | ==Triangles with angles of <math>60^\circ</math> or <math>120^\circ</math>== | ||
| Line 87: | Line 232: | ||
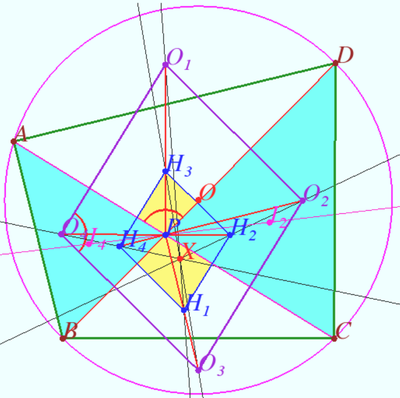
==Euler lines of cyclic quadrilateral (Vittas’s theorem)== | ==Euler lines of cyclic quadrilateral (Vittas’s theorem)== | ||
| + | <i><b>Claim 1</b></i> | ||
[[File:2 chords 4 triangles 1.png|400px|right]] | [[File:2 chords 4 triangles 1.png|400px|right]] | ||
| − | Let <math>ABCD</math> be a cyclic quadrilateral with diagonals intersecting at <math>P (\angle APB \ne 60^\circ).</math> | + | Let <math>ABCD</math> be a cyclic quadrilateral with diagonals intersecting at <math>P (\angle APB \ne 60^\circ).</math> The Euler lines of triangles <math>\triangle APB, \triangle BPC, \triangle CPD, \triangle DPA</math> are concurrent. |
<i><b>Proof</b></i> | <i><b>Proof</b></i> | ||
| Line 106: | Line 252: | ||
We use <i><b>Claim</b></i> and get that lines <math>O_1H_1, O_2H_2, O_3H_3, O_4H_4</math> are concurrent (or parallel if <math>\angle APD = 60^\circ</math> or <math>\angle APD = 120^\circ</math>). | We use <i><b>Claim</b></i> and get that lines <math>O_1H_1, O_2H_2, O_3H_3, O_4H_4</math> are concurrent (or parallel if <math>\angle APD = 60^\circ</math> or <math>\angle APD = 120^\circ</math>). | ||
| − | <i><b>Claim (Property of vertex of two parallelograms)</b></i> | + | <i><b>Claim 2 (Property of vertex of two parallelograms)</b></i> |
[[File:2 parallelograms.png|400px|right]] | [[File:2 parallelograms.png|400px|right]] | ||
Let <math>ABCD</math> and <math>EFGH</math> be parallelograms, <math>AB||EF, AD||EH.</math> Let lines <math>AE, BH,</math> and <math>CG</math> be concurrent at point <math>O.</math> Then points <math>D, O,</math> and <math>F</math> are collinear and lines <math>AG, BF, CE,</math> and <math>DH</math> are concurrent. | Let <math>ABCD</math> and <math>EFGH</math> be parallelograms, <math>AB||EF, AD||EH.</math> Let lines <math>AE, BH,</math> and <math>CG</math> be concurrent at point <math>O.</math> Then points <math>D, O,</math> and <math>F</math> are collinear and lines <math>AG, BF, CE,</math> and <math>DH</math> are concurrent. | ||
| Line 126: | Line 272: | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ~minor edit by Yiyj1 | ||
==Concurrent Euler lines and Fermat points== | ==Concurrent Euler lines and Fermat points== | ||
| Line 257: | Line 404: | ||
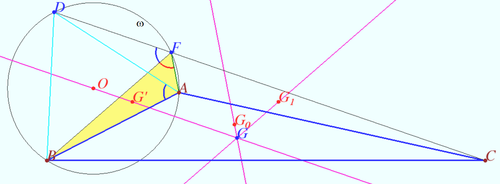
==Thebault point== | ==Thebault point== | ||
| − | [[File:Orthic triangle.png| | + | [[File:Orthic triangle.png|400px|right]] |
Let <math>AD, BE,</math> and <math>CF</math> be the altitudes of the <math>\triangle ABC,</math> where <math>BC> AC > AB, \angle BAC \ne 90^\circ.</math> | Let <math>AD, BE,</math> and <math>CF</math> be the altitudes of the <math>\triangle ABC,</math> where <math>BC> AC > AB, \angle BAC \ne 90^\circ.</math> | ||
| Line 306: | Line 453: | ||
<i><b>Case 2 Obtuse triangle</b></i> | <i><b>Case 2 Obtuse triangle</b></i> | ||
| − | [[File:Orthic triangle obtuse.png| | + | [[File:Orthic triangle obtuse.png|400px|right]] |
a) It is known, that Euler line of obtuse <math>\triangle ABC</math> cross AC and BC (middle and longest sides) in inner points. | a) It is known, that Euler line of obtuse <math>\triangle ABC</math> cross AC and BC (middle and longest sides) in inner points. | ||
| Line 345: | Line 492: | ||
<i><b>Claim (Segment crossing the median)</b></i> | <i><b>Claim (Segment crossing the median)</b></i> | ||
| − | [[File:Median cross segment.png| | + | [[File:Median cross segment.png|400px|right]] |
Let <math>M</math> be the midpoint of side <math>AB</math> of the <math>\triangle ABC, D \in AC,</math> | Let <math>M</math> be the midpoint of side <math>AB</math> of the <math>\triangle ABC, D \in AC,</math> | ||
| − | < | + | <cmath>E \in BC, G = DE \cap CM.</cmath> |
| + | <cmath>\frac {BE}{CE} = m, \frac {AD}{CD} = n.</cmath> | ||
Then <math>\frac {DG}{GE} = \frac{1+m}{1+n}, \frac {MG}{GC} = \frac{n+m}{2}.</math> | Then <math>\frac {DG}{GE} = \frac{1+m}{1+n}, \frac {MG}{GC} = \frac{n+m}{2}.</math> | ||
| Line 364: | Line 512: | ||
x = \frac{1}{(1+n)(2+m+n)}.</cmath> | x = \frac{1}{(1+n)(2+m+n)}.</cmath> | ||
<cmath>z+x = \frac {[CDM]}{2[CAM]} = \frac {1}{2(1 + n)}.</cmath> | <cmath>z+x = \frac {[CDM]}{2[CAM]} = \frac {1}{2(1 + n)}.</cmath> | ||
| − | <cmath>\frac {MG}{GC} = \frac {z}{x} = \frac {z + x}{x} | + | <cmath>\frac {MG}{GC} = \frac {z}{x} = \frac {z + x}{x} - 1 =\frac {1}{2(1 + n)} (1 + n)(2 + m + n) - 1 = \frac {n + m}{2}.</cmath> |
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
==Schiffler point== | ==Schiffler point== | ||
| − | [[File:Shiffler point.png| | + | [[File:Shiffler point.png|400px|right]] |
Let <math>I, O, G, R, \alpha,</math> and <math>r</math> be the incenter, circumcenter, centroid, circumradius, <math>\angle A,</math> and inradius of <math>\triangle ABC,</math> respectively. Then the Euler lines of the four triangles <math>\triangle BCI, \triangle CAI, \triangle ABI,</math> and <math>\triangle ABC</math> are concurrent at Schiffler point <math>S = X(21), \frac {OS}{SG} = \frac {3R}{2r}</math>. | Let <math>I, O, G, R, \alpha,</math> and <math>r</math> be the incenter, circumcenter, centroid, circumradius, <math>\angle A,</math> and inradius of <math>\triangle ABC,</math> respectively. Then the Euler lines of the four triangles <math>\triangle BCI, \triangle CAI, \triangle ABI,</math> and <math>\triangle ABC</math> are concurrent at Schiffler point <math>S = X(21), \frac {OS}{SG} = \frac {3R}{2r}</math>. | ||
| Line 390: | Line 538: | ||
<cmath>m = \frac {GX}{XE} = \frac {2n}{3}.</cmath> | <cmath>m = \frac {GX}{XE} = \frac {2n}{3}.</cmath> | ||
| − | <cmath>p = \frac {OE}{EY} = \frac {\cos \alpha}{(1 | + | <cmath>p = \frac {OE}{EY} = \frac {\cos \alpha}{(1 - \cos \alpha)/3} = \frac {3 \cos \alpha}{1 - \cos \alpha}</cmath> |
Using <i><b>Claim</b></i> we get | Using <i><b>Claim</b></i> we get | ||
| − | <cmath>\frac {OS}{SG} = \frac {p+1}{m} | + | <cmath>\frac {OS}{SG} = \frac {p + 1}{m} - \frac {p}{n} = \frac {3(p + 1)}{2n} - \frac {p}{n} = \frac {p + 3}{2n} = \frac {3R}{2r}.</cmath> |
Therefore each Euler line of triangles <math>\triangle BCI, \triangle CAI, \triangle ABI,</math> cross Euler line of <math>\triangle ABC</math> in the same point, as desired. | Therefore each Euler line of triangles <math>\triangle BCI, \triangle CAI, \triangle ABI,</math> cross Euler line of <math>\triangle ABC</math> in the same point, as desired. | ||
<i><b>Claim (Segments crossing inside triangle)</b></i> | <i><b>Claim (Segments crossing inside triangle)</b></i> | ||
| − | [[File:Segments crossing inside triangle.png| | + | [[File:Segments crossing inside triangle.png|400px|right]] |
Given triangle GOY. Point <math>S</math> lies on <math>GO, k = \frac {OS}{SG}.</math> | Given triangle GOY. Point <math>S</math> lies on <math>GO, k = \frac {OS}{SG}.</math> | ||
| Line 404: | Line 552: | ||
Point <math>G'</math> lies on <math>GY, n = \frac {GG'}{G'Y}.</math> | Point <math>G'</math> lies on <math>GY, n = \frac {GG'}{G'Y}.</math> | ||
| − | Point <math>X</math> lies on <math>GE, m = \frac {GX}{XE}.</math> Then <math>k = \frac {p+1}{m} | + | Point <math>X</math> lies on <math>GE, m = \frac {GX}{XE}.</math> Then <math>k = \frac {p + 1}{m} - \frac {p}{n}.</math> |
<i><b>Proof</b></i> | <i><b>Proof</b></i> | ||
Let <math>[OGY]</math> be <math>1</math> (We use sigh <math>[t]</math> for area of <math>t).</math> | Let <math>[OGY]</math> be <math>1</math> (We use sigh <math>[t]</math> for area of <math>t).</math> | ||
| − | <cmath>[GSG'] = \frac{n}{(n+1)(k+1)}, [YEG'] = \frac{1}{(n+1)(p+1)},</cmath> | + | <cmath>[GSG'] = \frac{n}{(n + 1)(k + 1)}, [YEG'] = \frac{1}{(n + 1)(p + 1)},</cmath> |
| − | <cmath>[SOE] = \frac{kp}{(k+1)(p+1)}, [ESG'] = \frac {[GSG']}{m},</cmath> | + | <cmath>[SOE] = \frac{kp}{(k + 1)(p + 1)}, [ESG'] = \frac {[GSG']}{m},</cmath> |
| − | <cmath>[OGY] = [GSG'] + [YEG'] + [SOE] + [ESG'] = 1 \implies \frac{n(p+1)}{m}=nk + p \implies k = \frac {p+1}{m} | + | <cmath>[OGY] = [GSG'] + [YEG'] + [SOE] + [ESG'] = 1 \implies</cmath> |
| + | <cmath>\frac{n(p + 1)}{m}=nk + p \implies k = \frac {p + 1}{m} - \frac {p}{n}.</cmath> | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| − | ==Euler line as radical | + | ==Euler line as radical axis== |
[[File:3 circles Euler line.png|500px|right]] | [[File:3 circles Euler line.png|500px|right]] | ||
Let <math>\triangle ABC</math> with altitudes <math>AA_1, BB_1,</math> and <math>CC_1</math> be given. | Let <math>\triangle ABC</math> with altitudes <math>AA_1, BB_1,</math> and <math>CC_1</math> be given. | ||
| Line 442: | Line 591: | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| − | ==De Longchamps point | + | ==De Longchamps point X(20)== |
| − | [[File:Longchamps.png| | + | [[File:Longchamps.png|400px|right]] |
<i><b>Definition 1</b></i> | <i><b>Definition 1</b></i> | ||
| − | The De Longchamps’ point of a triangle is the radical center of the power circles of the triangle. | + | The De Longchamps’ point of a triangle is the radical center of the power circles of the triangle. Prove that De Longchamps point lies on Euler line. |
| + | |||
We call A-power circle of a <math>\triangle ABC</math> the circle centered at the midpoint <math>BC</math> point <math>A'</math> with radius <math>R_A = AA'.</math> The other two circles are defined symmetrically. | We call A-power circle of a <math>\triangle ABC</math> the circle centered at the midpoint <math>BC</math> point <math>A'</math> with radius <math>R_A = AA'.</math> The other two circles are defined symmetrically. | ||
| Line 462: | Line 612: | ||
Point <math>E</math> is the crosspoint of the center line of the <math>B-</math>power and <math>C-</math>power circles and there radical axis. <math>B'C' = \frac {a}{2}.</math> We use claim and get: | Point <math>E</math> is the crosspoint of the center line of the <math>B-</math>power and <math>C-</math>power circles and there radical axis. <math>B'C' = \frac {a}{2}.</math> We use claim and get: | ||
| − | <cmath>C'E = \frac {a}{4} + \frac {R_C^2 | + | <cmath>C'E = \frac {a}{4} + \frac {R_C^2 - R_B^2}{a}.</cmath> |
<math>R_B</math> and <math>R_C</math> are the medians, so | <math>R_B</math> and <math>R_C</math> are the medians, so | ||
| − | <cmath>R_B^2 = \frac {a^2}{2}+ \frac {c^2}{2} | + | <cmath>R_B^2 = \frac {a^2}{2}+ \frac {c^2}{2} - \frac {b^2}{4}, R_C^2 = \frac {a^2}{2}+ \frac {b^2}{2} - \frac {c^2}{4} \implies C'E = \frac {a}{4} + \frac {3(b^2 - c^2)}{4a}.</cmath> |
We use Claim some times and get: | We use Claim some times and get: | ||
| − | <cmath>C'A_t = \frac {a}{4} | + | <cmath>C'A_t = \frac {a}{4} - \frac {b^2 - c^2}{4a}, |
| − | A_tO_t = \frac {a}{2} | + | A_tO_t = \frac {a}{2} - 2 C'A_t = \frac {b^2 - c^2}{2a} \implies</cmath> |
| − | <cmath> | + | <cmath>O_t L_t = C'E - C'A_t - A_t O_t = \frac {b^2 - c^2}{2a} = A_t O_t = H_t O_t \implies</cmath> |
radical axes of <math>B-</math>power and <math>C-</math>power cicles is symmetric to altitude <math>AH</math> with respect <math>O.</math> | radical axes of <math>B-</math>power and <math>C-</math>power cicles is symmetric to altitude <math>AH</math> with respect <math>O.</math> | ||
Similarly radical axes of <math>A-</math>power and <math>B-</math>power cicles is symmetric to altitude <math>CH,</math> radical axes of <math>A-</math>power and <math>C-</math>power cicles is symmetric to altitude <math>BH</math> with respect <math>O.</math> | Similarly radical axes of <math>A-</math>power and <math>B-</math>power cicles is symmetric to altitude <math>CH,</math> radical axes of <math>A-</math>power and <math>C-</math>power cicles is symmetric to altitude <math>BH</math> with respect <math>O.</math> | ||
| − | Therefore the point of intersection of the radical axes, symmetrical to the heights with respect to O, is symmetrical to the point of intersection of the heights with respect to <math>O \implies \vec {HO} = \vec {OL} \implies L</math> lies on Euler line of <math>\triangle ABC.</math> | + | Therefore the point <math>L</math> of intersection of the radical axes, symmetrical to the heights with respect to <math>O,</math> is symmetrical to the point <math>H</math> of intersection of the heights with respect to <math>O \implies \vec {HO} = \vec {OL} \implies L</math> lies on Euler line of <math>\triangle ABC.</math> |
| + | [[File:Distances.png|350px|right]] | ||
| + | <i><b>Claim (Distance between projections)</b></i> | ||
| + | |||
| + | <cmath>x + y = a, c^2 - x^2 = h^2 = b^2 - y^2,</cmath> | ||
| + | <cmath>y^2 - x^2 = b^2 - c^2 \implies y - x = \frac {b^2 - c^2}{a},</cmath> | ||
| + | <cmath>x = \frac {a}{2} - \frac {b^2 - c^2}{2a}, y = \frac {a}{2} + \frac {b^2 - c^2}{2a}.</cmath> | ||
| + | |||
| + | <i><b>Definition 2</b></i> | ||
| + | [[File:Longchamps 1.png|400px|right]] | ||
| + | We call <math>\omega_A = A-</math>circle of a <math>\triangle ABC</math> the circle centered at <math>A</math> with radius <math>BC.</math> The other two circles are defined symmetrically. The De Longchamps point of a triangle is the radical center of <math>A-</math>circle, <math>B-</math>circle, and <math>C-</math>circle of the triangle (Casey – 1886). Prove that De Longchamps point under this definition is the same as point under <i><b>Definition 1.</b></i> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let <math>H, G,</math> and <math>L_o</math> be orthocenter, centroid, and De Longchamps point, respectively. Let <math>\omega_B</math> cross <math>\omega_C</math> at points <math>A'</math> and <math>E.</math> The other points <math>(D, F, B', C')</math> are defined symmetrically. | ||
| + | <cmath>AB' = BC, B'C = AB \implies \triangle ABC = \triangle CB'A \implies</cmath> | ||
| + | <cmath>AB||B'C \implies CH \perp B'C.</cmath> | ||
| + | Similarly <math>CH \perp A'C \implies A'B'</math> is diameter <math>\omega_C \implies</math> | ||
| + | <cmath>\angle A'EB' = 90^\circ, 2\vec {BG} = \vec {GB'}.</cmath> | ||
| + | |||
| + | Therefore <math>\triangle A'B'C'</math> is anticomplementary triangle of <math>\triangle ABC, \triangle DEF</math> is orthic triangle of <math>\triangle A'B'C'.</math> So <math>L_o</math> is orthocenter of <math>\triangle A'B'C'.</math> | ||
| + | |||
| + | <math>2\vec {HG} = \vec GL_o, 2\vec {GO} = \vec HG \implies L_o = L</math> as desired. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==De Longchamps line== | ||
| + | [[File:Longchamps lime.png|450px|right]] | ||
| + | The de Longchamps line <math>l</math> of <math>\triangle ABC</math> is defined as the radical axes of the de Longchamps circle <math>\omega</math> and of the circumscribed circle <math>\Omega</math> of <math>\triangle ABC.</math> | ||
| + | |||
| + | Let <math>\Omega'</math> be the circumcircle of <math>\triangle DEF</math> (the anticomplementary triangle of <math>\triangle ABC).</math> | ||
| + | |||
| + | Let <math>\omega'</math> be the circle centered at <math>G</math> (centroid of <math>\triangle ABC</math>) with radius <math>\rho = \frac {\sqrt{2}}{3} \sqrt {a^2 + b^2 + c^2},</math> where <math>a = BC, b = AC, c = AB.</math> | ||
| + | |||
| + | Prove that the de Longchamps line is perpendicular to Euler line and is the radical axes of <math>\Omega, \Omega', \omega,</math> and <math>\omega'.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Center of <math>\Omega</math> is <math>O</math>, center of <math>\omega</math> is <math>L \implies OL \perp l,</math> where <math>OL</math> is Euler line. | ||
| + | The homothety with center <math>G</math> and ratio <math>-2</math> maps <math>\triangle ABC</math> into <math>\triangle DEF.</math> This homothety maps <math>\Omega</math> into <math>\Omega'.</math> | ||
| + | <math>R_{\Omega} \ne R_{\Omega'}</math> and <math>\Omega \cap \Omega' = K \implies </math> there is two inversion which swap <math>\Omega</math> and <math>\Omega'.</math> | ||
| + | |||
| + | First inversion <math>I_{\omega'}</math> centered at point <math>G = \frac {\vec O \cdot 2R + \vec H \cdot R}{2R + R} = \frac {2\vec O + \vec H}{3}.</math> Let <math>K</math> be the point of crossing <math>\Omega</math> and <math>\Omega'.</math> | ||
| + | |||
| + | The radius of <math>\omega'</math> we can find using <math>\triangle HKO:</math> | ||
| + | |||
| + | <cmath>OK = R, HK = 2R, HG = 2GO \implies GK^2 = 2(R^2 – GO^2), GO^2 = \frac {HO^2}{9} \implies</cmath> | ||
| + | <cmath>R_G = GK = \frac {\sqrt {2(a^2 + b^2 + c^2)}}{3}.</cmath> | ||
| + | |||
| + | Second inversion <math>I_{\omega}</math> centered at point <math>L = \frac {\vec O \cdot 2R – \vec H \cdot R}{2R – R} = 2 \vec O – \vec H.</math> We can make the same calculations and get <math>R_L = 4R \sqrt{– \cos A \cos B \cos C}</math> as desired. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==CIRCUMCENTER OF THE TANGENTIAL TRIANGLE X(26)== | ||
| + | [[File:X26.png|400px|right]] | ||
| + | Prove that the circumcenter of the tangential triangle <math>\triangle A'B'C'</math> of <math>\triangle ABC</math> (Kimberling’s point <math>X(26))</math> lies on the Euler line of <math>\triangle ABC.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let <math>A_0, B_0,</math> and <math>C_0</math> be midpoints of <math>BC, AC,</math> and <math>AB,</math> respectively. | ||
| + | |||
| + | Let <math>\omega</math> be circumcircle of <math>\triangle A_0B_0C_0.</math> It is nine-points circle of the <math>\triangle ABC.</math> | ||
| + | |||
| + | Let <math>\Omega</math> be circumcircle of <math>\triangle ABC.</math> Let <math>\Omega'</math> be circumcircle of <math>\triangle A'B'C'.</math> | ||
| + | |||
| + | <math>A'B</math> and <math>A'C</math> are tangents to <math>\Omega \implies</math> inversion with respect <math>\Omega</math> swap <math>B'</math> and <math>B_0.</math> Similarly, this inversion swap <math>A'</math> and <math>A_0, C'</math> and <math>C_0.</math> Therefore this inversion swap <math>\omega</math> and <math>\Omega'.</math> | ||
| + | |||
| + | The center <math>N</math> of <math>\omega</math> and the center <math>O</math> of <math>\Omega</math> lies on Euler line, so the center <math>O'</math> of <math>\Omega'</math> lies on this line, as desired. | ||
| + | |||
| + | After some calculations one can find position of point <math>X(26)</math> on Euler line (see Kimberling's point <math>X(26)).</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==PERSPECTOR OF ORTHIC AND TANGENTIAL TRIANGLES X(25)== | ||
| + | [[File:X25.png|400px|right]] | ||
| + | Let <math>\triangle A_1B_1C_1</math> be the orthic triangle of <math>\triangle ABC. </math> Let <math>N</math> be the circumcenter of <math>\triangle A_1B_1C_1.</math> | ||
| + | Let <math>\triangle A'B'C'</math> be the tangencial triangle of <math>\triangle ABC.</math> Let <math>O'</math> be the circumcenter of <math>\triangle A'B'C'.</math> | ||
| + | |||
| + | Prove that lines <math>A_1A', B_1B',</math> and <math>C_1C'</math> are concurrent at point, lies on Euler line of <math>\triangle ABC.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | <math>B'C'</math> and <math>B_1C_1</math> are antiparallel to BC with respect <math>\angle BAC \implies B'C' ||B_1C_1.</math> | ||
| + | |||
| + | Similarly, <math>A'C' ||A_1C_1, A'B' ||A_1B_1.</math> | ||
| + | |||
| + | Therefore <math>\triangle A_1B_1C_1 \sim \triangle A'B'C' \implies</math> homothetic center of <math>\triangle A_1B_1C_1</math> and <math>\triangle A'B'C'</math> is the point of concurrence of lines <math>A_1A', B_1B',</math> and <math>C_1C'.</math> Denote this point as <math>K.</math> | ||
| + | |||
| + | The points <math>N</math> and <math>O'</math> are the corresponding points (circumcenters) of <math>\triangle A_1B_1C_1</math> and <math>\triangle A'B'C',</math> so point <math>K</math> lies on line <math>NO'.</math> | ||
| + | |||
| + | Points <math>N</math> and <math>O' = X(26)</math> lies on Euler line, so <math>K</math> lies on Euler line of <math>\triangle ABC.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Exeter point X(22)== | ||
| + | [[File:Exeter X22.png|400px|right]] | ||
| + | Exeter point is the perspector of the circummedial triangle <math>A_0B_0C_0</math> and the tangential triangle <math>A'B'C'.</math> By another words, let <math>\triangle ABC</math> be the reference triangle (other than a right triangle). Let the medians through the vertices <math>A, B, C</math> meet the circumcircle <math>\Omega</math> of triangle <math>ABC</math> at <math>A_0, B_0,</math> and <math>C_0</math> respectively. Let <math>A'B'C'</math> be the triangle formed by the tangents at <math>A, B,</math> and <math>C</math> to <math>\Omega.</math> (Let <math>A'</math> be the vertex opposite to the side formed by the tangent at the vertex A). Prove that the lines through <math>A_0A', B_0B',</math> and <math>C_0C'</math> are concurrent, the point of concurrence lies on Euler line of triangle <math>ABC,</math> the point of concurrence <math>X_{22}</math> lies on Euler line of triangle <math>ABC, \vec {X_{22}} = \vec O + \frac {2}{J^2 - 3} (\vec H - \vec O), J = \frac {|OH|}{R},</math> where <math>O</math> - circumcenter, <math>H</math> - orthocenter, <math>R</math> - circumradius. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | At first we prove that lines <math>A_0A', B_0B',</math> and <math>C_0C'</math> are concurrent. This follows from the fact that lines <math>AA_0, BB_0,</math> and <math>CC_0</math> are concurrent at point <math>G</math> and <i><b>Mapping theorem</b></i>. | ||
| + | |||
| + | Let <math>A_1, B_1,</math> and <math>C_1</math> be the midpoints of <math>BC, AC,</math> and <math>AB,</math> respectively. The points <math>A, G, A_1,</math> and <math>A_0</math> are collinear. Similarly the points <math>B, G, B_1,</math> and <math>B_0</math> are collinear. | ||
| + | |||
| + | Denote <math>I_{\Omega}</math> the inversion with respect <math>\Omega.</math> It is evident that <math>I_{\Omega}(A_0) = A_0, I_{\Omega}(A') = A_1, I_{\Omega}(B_0) = B_0, I_{\Omega}(B') = B_1.</math> | ||
| + | |||
| + | Denote <math>\omega_A = I_{\Omega}(A'A_0), \omega_B = I_{\Omega}(B'B_0) \implies</math> | ||
| + | <cmath>A_0 \in \omega_A, A_1 \in \omega_A, O \in \omega_A, B_0 \in \omega_B, B_1 \in \omega_B, O \in \omega_B \implies O = \omega_A \cap \omega_B.</cmath> | ||
| + | |||
| + | The power of point <math>G</math> with respect <math>\omega_A</math> is <math>GA_1 \cdot GA_0 = \frac {1}{2} AG \cdot GA_0.</math> | ||
| + | |||
| + | Similarly the power of point <math>G</math> with respect <math>\omega_B</math> is <math>GB_1 \cdot GB_0 = \frac {1}{2} BG \cdot GB_0.</math> | ||
| + | |||
| + | <math>G = BB_0 \cap AA_0 \implies AG \cdot GA_0 = BG \cdot GB_0 \implies G</math> lies on radical axis of <math>\omega_A</math> and <math>\omega_B.</math> | ||
| + | |||
| + | Therefore second crosspoint of <math>\omega_A</math> and <math>\omega_B</math> point <math>D</math> lies on line <math>OG</math> which is the Euler line of <math>\triangle ABC.</math> | ||
| + | Point <math>X_{22} = I_{\Omega}(D)</math> lies on the same Euler line as desired. | ||
| + | |||
| + | Last we will find the length of <math>OX_{22}.</math> | ||
| + | <cmath>A_1 = BC \cap AA_0 \implies AA_1 \cdot A_1A_0 = BA_1 \cdot CA_1 = \frac {BC^2}{4}.</cmath> | ||
| + | <cmath>GO \cdot GD =GO \cdot (GO + OD) = GA_1 \cdot GA_0</cmath> | ||
| + | <cmath>GA_1 \cdot GA_0 = \frac {AA_1}{3} \cdot ( \frac {AA_1}{3} + A_1A_0) = \frac {AA_1^2}{9} + | ||
| + | \frac {BC^2}{3 \cdot 4} = \frac {AB^2 + BC^2 + AC^2}{18}= \frac {R^2 - GO^2} {2}.</cmath> | ||
| + | <cmath>2GO^2 + 2 GO \cdot OD = R^2 - GO^2 \implies 2 GO \cdot OD = R^2 - 3GO^2.</cmath> | ||
| + | <cmath> I_{\Omega}(D) = X_{22} \implies OX_{22} = \frac {R^2} {OD} | ||
| + | = \frac {R^2 \cdot 2 GO}{R^2 - 3 GO^2} = \frac {2 HO}{3 - \frac {HO^2}{R^2}} = \frac {2}{3 - J^2} HO</cmath> as desired. | ||
| + | |||
| + | <i><b>Mapping theorem</b></i> | ||
| + | [[File:Transformation.png|400px|right]] | ||
| + | Let triangle <math>ABC</math> and incircle <math>\omega</math> be given. | ||
| + | <cmath>D = BC \cap \omega, E = AC \cap \omega, F = AB \cap \omega.</cmath> | ||
| + | Let <math>P</math> be the point in the plane <math>ABC.</math> | ||
| + | Let lines <math>DP, EP,</math> and <math>FP</math> crossing <math>\omega</math> second time at points <math>D_0, E_0,</math> and <math>F_0,</math> respectively. | ||
| + | |||
| + | Prove that lines <math>AD_0, BE_0, </math> and <math>CF_0</math> are concurrent. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | <cmath>k_A = \frac {\sin {D_0AE'}}{\sin {D_0AF'}} = \frac {D_0E'}{D_0A} \cdot \frac {D_0A}{D_0F'} = \frac {D_0E'}{D_0F'}.</cmath> | ||
| + | We use Claim and get: <math>k_A = \frac {D_0E^2}{D_0F^2}.</math> | ||
| + | <cmath>k_D = \frac {\sin {D_0DE}}{\sin {D_0DF}} = \frac {D_0E}{2R} \cdot \frac {2R}{D_0F} = \frac {D_0E}{D_0F} \implies k_A = k_D^2.</cmath> | ||
| + | Similarly, <math>k_B = k_E^2, k_C = k_F^2.</math> | ||
| + | |||
| + | We use the trigonometric form of Ceva's Theorem for point <math>P</math> and triangle <math>\triangle DEF</math> and get | ||
| + | <cmath>k_D \cdot k_E \cdot k_F = 1 \implies k_A \cdot k_B \cdot k_C = 1^2 = 1.</cmath> | ||
| + | We use the trigonometric form of Ceva's Theorem for triangle <math>\triangle ABC</math> and finish proof that lines <math>AD_0, BE_0, </math> and <math>CF_0</math> are concurrent. | ||
| + | |||
| + | |||
| + | <i><b>Claim (Point on incircle)</b></i> | ||
| + | [[File:Point on incircle.png|400px|right]] | ||
| + | Let triangle <math>ABC</math> and incircle <math>\omega</math> be given. | ||
| + | <cmath>D = BC \cap \omega, E = AC \cap \omega, F = AB \cap \omega, P \in \omega, F' \in AB,</cmath> | ||
| + | <cmath>PF' \perp AB, E' \in AC, PE' \perp AC, A' \in EF, PA' \perp EF.</cmath> | ||
| + | Prove that <math>\frac {PF'}{PE'} = \frac {PF^2}{PE^2}, PA'^2 = PF' \cdot PE'.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | <cmath>AF = AE \implies \angle AFE = \angle AEF = \angle A'EE'.</cmath> | ||
| + | <cmath>\angle EFP = \angle PEE' \implies \angle PFF' = \angle PEE' \implies</cmath> | ||
| + | <cmath>\triangle PFF' \sim \triangle PEA' \implies \frac {PF}{PF'} = \frac {PE}{PA'}.</cmath> | ||
| + | |||
| + | Similarly <math>\triangle PEE' \sim \triangle PFA' \implies \frac {PE}{PE'} = \frac {PF}{PA'}.</math> | ||
| + | |||
| + | We multiply and divide these equations and get: | ||
| + | <cmath>PA'^2 = PF' \cdot PE', \frac {PF'}{PE'} = \frac {PF^2}{PE^2}.</cmath> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Far-out point X(23)== | ||
| + | [[File:Far-out point X23.png|400px|right]] | ||
| + | Let <math>\triangle A'B'C'</math> be the tangential triangle of <math>\triangle ABC.</math> | ||
| + | |||
| + | Let <math>G, \Omega, O, R,</math> and <math>H</math> be the centroid, circumcircle, circumcenter, circumradius and orthocenter of <math>\triangle ABC.</math> | ||
| + | |||
| + | Prove that the second crosspoint of circumcircles of <math>\triangle AA'O, \triangle BB'O,</math> and <math>\triangle CC'O</math> is point <math>X_{23}.</math> Point <math>X_{23}</math> lies on Euler line of <math>\triangle ABC, X_{23} = O + \frac {3}{J^2} (H – O), J = \frac {OH}{R}.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Denote <math>I_{\Omega}</math> the inversion with respect <math>\Omega, A_1, B_1, C_1</math> midpoints of <math>BC, AC, AB.</math> | ||
| + | |||
| + | It is evident that <math>I_{\Omega}(A') = A_1, I_{\Omega}(B') = B_1, I_{\Omega}(C') = C_1.</math> | ||
| + | |||
| + | The inversion of circles <math>AA'O, BB'O, CC'O</math> are lines <math>AA_1, BB_1,CC_1</math> which crosses at point <math>G \implies X_{23} = I_{\Omega}(G).</math> | ||
| + | |||
| + | Therefore point <math>X_{23}</math> lies on Euler line <math>OG</math> of <math>\triangle ABC, OG \cdot OX_{23} = R^2 \implies \frac {OX_{23}} {OH} = \frac {R^2}{OG \cdot OH} = \frac {3}{J^2},</math> as desired. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Symmetric lines== | ||
| + | [[File:H line.png|400px|right]] | ||
| + | Let triangle <math>ABC</math> having the circumcircle <math>\omega</math> be given. | ||
| + | |||
| + | Prove that the lines symmetric to the Euler line with respect <math>BC, AC,</math> and <math>AB</math> are concurrent and the point of concurrence lies on <math>\omega.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | The orthocenter <math>H</math> lies on the Euler line therefore the Euler line is <math>H-line.</math> We use <i><b>H-line Clime</b></i> and finish the proof. | ||
| + | |||
| + | ==H–line Claim== | ||
| + | |||
| + | Let triangle <math>ABC</math> having the orthocenter <math>H</math> and circumcircle <math>\omega</math> be given. Denote <math>H–line</math> any line containing point <math>H.</math> | ||
| + | |||
| + | Let <math>l_A, l_B,</math> and <math>l_C</math> be the lines symmetric to <math>H-line</math> with respect <math>BC, AC,</math> and <math>AB,</math> respectively. | ||
| + | |||
| + | Prove that <math>l_A, l_B,</math> and <math>l_C</math> are concurrent and the point of concurrence lies on <math>\omega.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let <math>D, E,</math> and <math>F</math> be the crosspoints of <math>H–line</math> with <math>AB, AC,</math> and <math>BC,</math> respectively. | ||
| + | |||
| + | WLOG <math>D \in AB, E \in AC.</math> | ||
| + | Let <math>H_A, H_B,</math> and <math>H_C</math> be the points symmetric to <math>H</math> with respect <math>BC, AC,</math> and <math>AB,</math> respectively. | ||
| + | |||
| + | Therefore <math>H_A \in l_A, H_B \in l_B, H_C \in l_C, AH = AH_B = AH_C, BH = BH_A = BH_C, CH = CH_A = CH_B \implies</math> | ||
| + | <cmath>\angle HH_BE = \angle EHH_B = \angle BHD = \angle BH_CD.</cmath> | ||
| + | |||
| + | Let <math>P</math> be the crosspoint of <math>l_B</math> and <math>l_C \implies BH_CH_BP</math> is cyclic <math>\implies P \in \omega.</math> | ||
| + | |||
| + | Similarly <math>\angle CH_BE = \angle CHE = \angle CH_A \implies CH_BH_AP</math> is cyclic <math>\implies P \in \omega \implies</math> the crosspoint of <math>l_B</math> and <math>l_A</math> is point <math>P.</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
==See also== | ==See also== | ||
*[[Kimberling center]] | *[[Kimberling center]] | ||
| + | *[[Kimberling’s point X(20)]] | ||
| + | *[[Kimberling’s point X(21)]] | ||
| + | *[[Kimberling’s point X(22)]] | ||
| + | *[[Kimberling’s point X(23)]] | ||
| + | *[[Kimberling’s point X(24)]] | ||
| + | *[[Kimberling’s point X(25)]] | ||
| + | *[[Kimberling’s point X(26)]] | ||
| + | *[[De Longchamps point]] | ||
| + | *[[Gossard perspector]] | ||
| + | *[[Evans point]] | ||
| + | *[[Double perspective triangles]] | ||
| + | *[[Steiner line]] | ||
| + | *[[Miquel's point]] | ||
| + | *[[Spieker center]] | ||
| + | *[[Simson line]] | ||
| + | *[[Complete Quadrilateral]] | ||
| + | *[[Gauss line]] | ||
| + | *[[Isogonal conjugate]] | ||
| + | *[[Barycentric coordinates]] | ||
| + | *[[Symmetry]] | ||
| + | *[[Symmedian and Antiparallel]] | ||
*[[Central line]] | *[[Central line]] | ||
| − | |||
*[[Gergonne line]] | *[[Gergonne line]] | ||
*[[Gergonne point]] | *[[Gergonne point]] | ||
| − | + | ||
{{stub}} | {{stub}} | ||
Latest revision as of 03:47, 30 August 2023
In any triangle ![]() , the Euler line is a line which passes through the orthocenter
, the Euler line is a line which passes through the orthocenter ![]() , centroid
, centroid ![]() , circumcenter
, circumcenter ![]() , nine-point center
, nine-point center ![]() and de Longchamps point
and de Longchamps point ![]() . It is named after Leonhard Euler. Its existence is a non-trivial fact of Euclidean geometry. Certain fixed orders and distance ratios hold among these points. In particular,
. It is named after Leonhard Euler. Its existence is a non-trivial fact of Euclidean geometry. Certain fixed orders and distance ratios hold among these points. In particular, ![]() and
and ![]()
Euler line is the central line ![]() .
.
Given the orthic triangle ![]() of
of ![]() , the Euler lines of
, the Euler lines of ![]() ,
,![]() , and
, and ![]() concur at
concur at ![]() , the nine-point circle of
, the nine-point circle of ![]() .
.
Contents
- 1 Proof Centroid Lies on Euler Line
- 2 Another Proof
- 3 Proof Nine-Point Center Lies on Euler Line
- 4 Analytic Proof of Existence
- 5 The points of intersection of the Euler line with the sides of the triangle
- 6 Angles between Euler line and the sides of the triangle
- 7 Distances along Euler line
- 8 Position of Kimberling centers on the Euler line
- 9 Triangles with angles of or
- 10 Euler lines of cyclic quadrilateral (Vittas’s theorem)
- 11 Concurrent Euler lines and Fermat points
- 12 Euler line of Gergonne triangle
- 13 Thebault point
- 14 Schiffler point
- 15 Euler line as radical axis
- 16 De Longchamps point X(20)
- 17 De Longchamps line
- 18 CIRCUMCENTER OF THE TANGENTIAL TRIANGLE X(26)
- 19 PERSPECTOR OF ORTHIC AND TANGENTIAL TRIANGLES X(25)
- 20 Exeter point X(22)
- 21 Far-out point X(23)
- 22 Symmetric lines
- 23 H–line Claim
- 24 See also
Proof Centroid Lies on Euler Line
This proof utilizes the concept of spiral similarity, which in this case is a rotation followed homothety. Consider the medial triangle ![]() . It is similar to
. It is similar to ![]() . Specifically, a rotation of
. Specifically, a rotation of ![]() about the midpoint of
about the midpoint of ![]() followed by a homothety with scale factor
followed by a homothety with scale factor ![]() centered at
centered at ![]() brings
brings ![]() . Let us examine what else this transformation, which we denote as
. Let us examine what else this transformation, which we denote as ![]() , will do.
, will do.
It turns out ![]() is the orthocenter, and
is the orthocenter, and ![]() is the centroid of
is the centroid of ![]() . Thus,
. Thus, ![]() . As a homothety preserves angles, it follows that
. As a homothety preserves angles, it follows that ![]() . Finally, as
. Finally, as ![]() it follows that
it follows that
![]() Thus,
Thus, ![]() are collinear, and
are collinear, and ![]() .
.
Another Proof
Let ![]() be the midpoint of
be the midpoint of ![]() .
Extend
.
Extend ![]() past
past ![]() to point
to point ![]() such that
such that ![]() . We will show
. We will show ![]() is the orthocenter.
Consider triangles
is the orthocenter.
Consider triangles ![]() and
and ![]() . Since
. Since ![]() , and they both share a vertical angle, they are similar by SAS similarity. Thus,
, and they both share a vertical angle, they are similar by SAS similarity. Thus, ![]() , so
, so ![]() lies on the
lies on the ![]() altitude of
altitude of ![]() . We can analogously show that
. We can analogously show that ![]() also lies on the
also lies on the ![]() and
and ![]() altitudes, so
altitudes, so ![]() is the orthocenter.
is the orthocenter.
Proof Nine-Point Center Lies on Euler Line
Assuming that the nine point circle exists and that ![]() is the center, note that a homothety centered at
is the center, note that a homothety centered at ![]() with factor
with factor ![]() brings the Euler points
brings the Euler points ![]() onto the circumcircle of
onto the circumcircle of ![]() . Thus, it brings the nine-point circle to the circumcircle. Additionally,
. Thus, it brings the nine-point circle to the circumcircle. Additionally, ![]() should be sent to
should be sent to ![]() , thus
, thus ![]() and
and ![]() .
.
Analytic Proof of Existence
Let the circumcenter be represented by the vector ![]() , and let vectors
, and let vectors ![]() correspond to the vertices of the triangle. It is well known the that the orthocenter is
correspond to the vertices of the triangle. It is well known the that the orthocenter is ![]() and the centroid is
and the centroid is ![]() . Thus,
. Thus, ![]() are collinear and
are collinear and ![]()
The points of intersection of the Euler line with the sides of the triangle
Acute triangle
Let ![]() be the acute triangle where
be the acute triangle where ![]() Denote
Denote ![]()
![]()
Let Euler line cross lines ![]() and
and ![]() in points
in points ![]() and
and ![]() respectively.
respectively.
Then point ![]() lyes on segment
lyes on segment ![]()
Point ![]() lyes on segment
lyes on segment ![]()
Point ![]() lyes on ray
lyes on ray ![]()
Proof
Denote ![]()
We use the formulae ![]() (see Claim “Segments crossing inside triangle” in “Schiffler point” in “Euler line”).
(see Claim “Segments crossing inside triangle” in “Schiffler point” in “Euler line”).
Centroid ![]() lyes on median
lyes on median ![]()
Orthocenter ![]() lyes on altitude
lyes on altitude ![]()
![]()
![]() Therefore
Therefore
![]()
![]() We use the signed version of Menelaus's theorem and get
We use the signed version of Menelaus's theorem and get
![]()
Obtuse triangle
Let ![]() be the obtuse triangle where
be the obtuse triangle where ![]()
Let Euler line cross lines ![]() and
and ![]() in points
in points ![]() and
and ![]() respectively.
respectively.
Similarly we get ![]()
![]()
![]() ray
ray ![]()
Right triangle
Let ![]() be the right triangle where
be the right triangle where ![]() Then Euler line contain median from vertex
Then Euler line contain median from vertex ![]()
Isosceles triangle
Let ![]() be the isosceles triangle where
be the isosceles triangle where ![]() Then Euler line contain median from vertex
Then Euler line contain median from vertex ![]()
Corollary: Euler line is parallel to side
Euler line ![]() is parallel to side
is parallel to side ![]() iff
iff ![]()
Proof
![]()
After simplification in the case ![]() we get
we get ![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
Angles between Euler line and the sides of the triangle
Let Euler line of the ![]() cross lines
cross lines ![]() and
and ![]() in points
in points ![]() and
and ![]() respectively.
Denote
respectively.
Denote ![]() smaller angles between the Euler line and lines
smaller angles between the Euler line and lines ![]() and
and ![]() as
as ![]() and
and ![]() respectively.
respectively.
Prove that ![]()
![]()
Proof
WLOG, ![]()
Let ![]() be the midpoint
be the midpoint ![]() be the circumcenter of
be the circumcenter of ![]()
![]()
![]()
![]()
Symilarly, for other angles.
vladimir.shelomovskii@gmail.com, vvsss
Distances along Euler line
Let ![]() and
and ![]() be orthocenter, centroid, circumcenter, and circumradius of the
be orthocenter, centroid, circumcenter, and circumradius of the ![]() respectively.
respectively.
![]()
![]()
Prove that ![]()
![]()
Proof
WLOG, ![]() is an acute triangle,
is an acute triangle, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Position of Kimberling centers on the Euler line
Let triangle ABC be given. Let ![]() and
and ![]() are orthocenter, circumcenter, circumradius and inradius, respectively.
are orthocenter, circumcenter, circumradius and inradius, respectively.
We use point ![]() as origin and
as origin and ![]() as a unit vector.
as a unit vector.
We find Kimberling center X(I) on Euler line in the form of
![]() For a lot of Kimberling centers the coefficient
For a lot of Kimberling centers the coefficient ![]() is a function of only two parameters
is a function of only two parameters ![]() and
and ![]()
Centroid ![]()
![]() Nine-point center
Nine-point center ![]()
![]() de Longchamps point
de Longchamps point ![]()
![]() Schiffler point
Schiffler point ![]()
![]() Exeter point
Exeter point ![]()
![]() Far-out point
Far-out point ![]()
![]() Perspector of ABC and orthic-of-orthic triangle
Perspector of ABC and orthic-of-orthic triangle ![]()
![]() Homothetic center of orthic and tangential triangles
Homothetic center of orthic and tangential triangles ![]()
![]() Circumcenter of the tangential triangle
Circumcenter of the tangential triangle ![]()
![]()
Midpoint of X(3) and ![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Triangles with angles of  or
or 
Claim 1
Let the ![]() in triangle
in triangle ![]() be
be ![]() Then the Euler line of the
Then the Euler line of the ![]() is parallel to the bisector of
is parallel to the bisector of ![]()
Proof
Let ![]() be circumcircle of
be circumcircle of ![]()
Let ![]() be circumcenter of
be circumcenter of ![]()
Let ![]() be the circle symmetric to
be the circle symmetric to ![]() with respect to
with respect to ![]()
Let ![]() be the point symmetric to
be the point symmetric to ![]() with respect to
with respect to ![]()
The ![]() lies on
lies on ![]() lies on
lies on ![]()
![]() is the radius of
is the radius of ![]() and
and ![]() translation vector
translation vector ![]() to
to ![]() is
is ![]()
Let ![]() be the point symmetric to
be the point symmetric to ![]() with respect to
with respect to ![]() Well known that
Well known that ![]() lies on
lies on ![]() Therefore point
Therefore point ![]() lies on
lies on ![]()
Point ![]() lies on
lies on ![]()
Let ![]() be the bisector of
be the bisector of ![]() are concurrent.
are concurrent.
![]()
Euler line ![]() of the
of the ![]() is parallel to the bisector
is parallel to the bisector ![]() of
of ![]() as desired.
as desired.
Claim 2
Let the ![]() in triangle
in triangle ![]() be
be ![]() Then the Euler line of the
Then the Euler line of the ![]() is perpendicular to the bisector of
is perpendicular to the bisector of ![]()
Proof
Let ![]() be circumcircle, circumcenter, orthocenter and incenter of the
be circumcircle, circumcenter, orthocenter and incenter of the ![]()
![]()
![]()
![]() points
points ![]() are concyclic.
are concyclic.
The circle ![]() centered at midpoint of small arc
centered at midpoint of small arc ![]()
![]() is rhomb.
is rhomb.
Therefore the Euler line ![]() is perpendicular to
is perpendicular to ![]() as desired.
as desired.
Claim 3
Let ![]() be a quadrilateral whose diagonals
be a quadrilateral whose diagonals ![]() and
and ![]() intersect at
intersect at ![]() and form an angle of
and form an angle of ![]() If the triangles PAB, PBC, PCD, PDA are all not equilateral, then their Euler lines are pairwise parallel or coincident.
If the triangles PAB, PBC, PCD, PDA are all not equilateral, then their Euler lines are pairwise parallel or coincident.
Proof
Let ![]() and
and ![]() be internal and external bisectors of the angle
be internal and external bisectors of the angle ![]() .
.
Then Euler lines of ![]() and
and ![]() are parallel to
are parallel to ![]() and Euler lines of
and Euler lines of ![]() and
and ![]() are perpendicular to
are perpendicular to ![]() as desired.
as desired.
vladimir.shelomovskii@gmail.com, vvsss
Euler lines of cyclic quadrilateral (Vittas’s theorem)
Claim 1
Let ![]() be a cyclic quadrilateral with diagonals intersecting at
be a cyclic quadrilateral with diagonals intersecting at ![]() The Euler lines of triangles
The Euler lines of triangles ![]() are concurrent.
are concurrent.
Proof
Let ![]() be the circumcenters (orthocenters) of triangles
be the circumcenters (orthocenters) of triangles ![]() Let
Let ![]() be the common bisector of
be the common bisector of ![]() and
and ![]()
![]()
![]()
![]()
![]() Therefore
Therefore ![]() and
and ![]() are parallelograms with parallel sides.
are parallelograms with parallel sides.
![]() bisect these angles.
So points
bisect these angles.
So points ![]() are collinear and lies on one straight line which is side of the pare vertical angles
are collinear and lies on one straight line which is side of the pare vertical angles ![]() and
and ![]() Similarly, points
Similarly, points ![]() are collinear and lies on another side of these angles.
Similarly obtuse
are collinear and lies on another side of these angles.
Similarly obtuse ![]() so points
so points ![]() and
and ![]() are collinear and lies on one side and points
are collinear and lies on one side and points ![]() and
and ![]() are collinear and lies on another side of the same vertical angles.
are collinear and lies on another side of the same vertical angles.
We use Claim and get that lines ![]() are concurrent (or parallel if
are concurrent (or parallel if ![]() or
or ![]() ).
).
Claim 2 (Property of vertex of two parallelograms)
Let ![]() and
and ![]() be parallelograms,
be parallelograms, ![]() Let lines
Let lines ![]() and
and ![]() be concurrent at point
be concurrent at point ![]() Then points
Then points ![]() and
and ![]() are collinear and lines
are collinear and lines ![]() and
and ![]() are concurrent.
are concurrent.
Proof
We consider only the case ![]() Shift transformation allows to generalize the obtained results.
Shift transformation allows to generalize the obtained results.
We use the coordinate system with the origin at the point ![]() and axes
and axes ![]()
We use ![]() and get
and get
![]()
![]()
![]() points
points ![]() and
and ![]() are colinear.
are colinear.
We calculate point of crossing ![]() and
and ![]() and
and ![]() and
and ![]() and get the same result:
and get the same result:
![]() as desired (if
as desired (if ![]() then point
then point ![]() moves to infinity and lines are parallel, angles
moves to infinity and lines are parallel, angles ![]() or
or ![]()
vladimir.shelomovskii@gmail.com, vvsss ~minor edit by Yiyj1
Concurrent Euler lines and Fermat points
Consider a triangle ![]() with Fermat–Torricelli points
with Fermat–Torricelli points ![]() and
and ![]() The Euler lines of the
The Euler lines of the ![]() triangles with vertices chosen from
triangles with vertices chosen from ![]() and
and ![]() are concurrent at the centroid
are concurrent at the centroid ![]() of triangle
of triangle ![]() We denote centroids by
We denote centroids by ![]() , circumcenters by
, circumcenters by ![]() We use red color for points and lines of triangles
We use red color for points and lines of triangles ![]() green color for triangles
green color for triangles ![]() and blue color for triangles
and blue color for triangles ![]()
Case 1
Let ![]() be the first Fermat point of
be the first Fermat point of ![]() maximum angle of which smaller then
maximum angle of which smaller then ![]() Then the centroid of triangle
Then the centroid of triangle ![]() lies on Euler line of the
lies on Euler line of the ![]() The pairwise angles between these Euler lines are equal
The pairwise angles between these Euler lines are equal ![]()
Proof
Let ![]() and
and ![]() be centroid, circumcenter, and circumcircle of
be centroid, circumcenter, and circumcircle of ![]() respectevely.
respectevely.
Let ![]() be external for
be external for ![]() equilateral triangle
equilateral triangle ![]()
![]() is cyclic.
is cyclic.
Point ![]() is centroid of
is centroid of ![]()
![]()
![]()
![]() Points
Points ![]() and
and ![]() are colinear, so point
are colinear, so point ![]() lies on Euler line
lies on Euler line ![]() of
of ![]()
![]()
Case 2
Let ![]() be the first Fermat point of
be the first Fermat point of ![]()
Then the centroid ![]() of triangle
of triangle ![]() lies on Euler lines of the triangles
lies on Euler lines of the triangles ![]() and
and ![]() The pairwise angles between these Euler lines are equal
The pairwise angles between these Euler lines are equal ![]()
Proof
Let ![]() be external for
be external for ![]() equilateral triangle,
equilateral triangle, ![]() be circumcircle of
be circumcircle of ![]()
![]() is cyclic.
is cyclic.
Point ![]() is centroid of
is centroid of ![]()
![]()
Points ![]() and
and ![]() are colinear, so point
are colinear, so point ![]() lies on Euler line
lies on Euler line ![]() of
of ![]() as desired.
as desired.
Case 3
Let ![]() be the second Fermat point of
be the second Fermat point of ![]() Then the centroid
Then the centroid ![]() of triangle
of triangle ![]() lies on Euler lines of the triangles
lies on Euler lines of the triangles ![]() and
and ![]()
The pairwise angles between these Euler lines are equal ![]()
Proof
Let ![]() be internal for
be internal for ![]() equilateral triangle,
equilateral triangle, ![]() be circumcircle of
be circumcircle of ![]()
Let ![]() and
and ![]() be circumcenters of the triangles
be circumcenters of the triangles ![]() and
and ![]() Point
Point ![]() is centroid of the
is centroid of the ![]() is the Euler line of the
is the Euler line of the ![]() parallel to
parallel to ![]()
![]() is bisector of
is bisector of ![]() is bisector of
is bisector of ![]() is bisector of
is bisector of ![]() is regular triangle.
is regular triangle.
![]() is the inner Napoleon triangle of the
is the inner Napoleon triangle of the ![]() is centroid of this regular triangle.
is centroid of this regular triangle.
![]()
![]() points
points ![]() and
and ![]() are collinear as desired.
are collinear as desired.
Similarly, points ![]() and
and ![]() are collinear.
are collinear.
Case 4
Let ![]() and
and ![]() be the Fermat points of
be the Fermat points of ![]() Then the centroid of
Then the centroid of ![]() point
point ![]() lies on Euler line
lies on Euler line ![]() is circumcenter,
is circumcenter, ![]() is centroid) of the
is centroid) of the ![]()
Proof
Step 1 We will find line ![]() which is parallel to
which is parallel to ![]()
Let ![]() be midpoint of
be midpoint of ![]() Let
Let ![]() be the midpoint of
be the midpoint of ![]()
Let ![]() be point symmetrical to
be point symmetrical to ![]() with respect to
with respect to ![]()
![]() as midline of
as midline of ![]()
![]()
![]()
Step 2 We will prove that line ![]() is parallel to
is parallel to ![]()
Let ![]() be the inner Napoleon triangle. Let
be the inner Napoleon triangle. Let ![]() be the outer Napoleon triangle. These triangles are regular centered at
be the outer Napoleon triangle. These triangles are regular centered at ![]()
Points ![]() and
and ![]() are collinear (they lies on bisector
are collinear (they lies on bisector ![]()
Points ![]() and
and ![]() are collinear (they lies on bisector
are collinear (they lies on bisector ![]()
Points ![]() and
and ![]() are collinear (they lies on bisector
are collinear (they lies on bisector ![]()
![]()
![]()
![]() angle between
angle between ![]() and
and ![]() is
is ![]()
![]()
Points ![]() and
and ![]() are concyclic
are concyclic ![]()
![]() Points
Points ![]() and
and ![]() are concyclic
are concyclic ![]()
![]() points
points ![]() and
and ![]() are concyclic
are concyclic
![]()
![]() Therefore
Therefore ![]() and
and ![]() are collinear or point
are collinear or point ![]() lies on Euler line
lies on Euler line ![]()
vladimir.shelomovskii@gmail.com, vvsss
Euler line of Gergonne triangle
Prove that the Euler line of Gergonne triangle of ![]() passes through the circumcenter of triangle
passes through the circumcenter of triangle ![]()
Gergonne triangle is also known as the contact triangle or intouch triangle. If the inscribed circle touches the sides of ![]() at points
at points ![]() and
and ![]() then
then ![]() is Gergonne triangle of
is Gergonne triangle of ![]() .
.
Other wording: Tangents to circumcircle of ![]() are drawn at the vertices of the triangle. Prove that the circumcenter of the triangle formed by these three tangents lies on the Euler line of the original triangle.
are drawn at the vertices of the triangle. Prove that the circumcenter of the triangle formed by these three tangents lies on the Euler line of the original triangle.
Proof
Let ![]() and
and ![]() be orthocenter and circumcenter of
be orthocenter and circumcenter of ![]() respectively.
Let
respectively.
Let ![]() be Orthic Triangle of
be Orthic Triangle of ![]()
Then ![]() is Euler line of
is Euler line of ![]()
![]() is the incenter of
is the incenter of ![]()
![]() is the incenter of
is the incenter of ![]()
![]()
Similarly, ![]()
![]() where
where ![]() is the perspector of triangles
is the perspector of triangles ![]() and
and ![]()
Under homothety with center P and coefficient ![]() the incenter
the incenter ![]() of
of ![]() maps into incenter
maps into incenter ![]() of
of ![]() , circumcenter
, circumcenter ![]() of
of ![]() maps into circumcenter
maps into circumcenter ![]() of
of ![]() are collinear as desired.
are collinear as desired.
vladimir.shelomovskii@gmail.com, vvsss
Thebault point
Let ![]() and
and ![]() be the altitudes of the
be the altitudes of the ![]() where
where ![]()
a) Prove that the Euler lines of triangles ![]() are concurrent on the nine-point circle at a point T (Thebault point of
are concurrent on the nine-point circle at a point T (Thebault point of ![]() )
)
b) Prove that if ![]() then
then ![]() else
else ![]()
Proof
Case 1 Acute triangle
a) It is known, that Euler line of acute triangle ![]() cross AB and BC (shortest and longest sides) in inner points.
cross AB and BC (shortest and longest sides) in inner points.
Let ![]() be circumcenters of
be circumcenters of ![]()
Let ![]() and
and ![]() be centroids of
be centroids of ![]()
Denote ![]() is the circle
is the circle ![]() (the nine-points circle).
(the nine-points circle).
![]() is the midpoint
is the midpoint ![]() where
where ![]() is the orthocenter of
is the orthocenter of ![]()
Similarly ![]()
![]() is the midline of
is the midline of ![]()
Let ![]() cross
cross ![]() at point
at point ![]() different from
different from ![]()
![]() spiral similarity centered at
spiral similarity centered at ![]() maps
maps ![]() onto
onto ![]()
This similarity has the rotation angle ![]() acute angle between Euler lines of these triangles is
acute angle between Euler lines of these triangles is ![]()
Let these lines crossed at point ![]() Therefore
Therefore ![]() points
points ![]() and
and ![]() are concyclic
are concyclic ![]()
Similarly, ![]() as desired.
as desired.
b) ![]() Point
Point ![]() lies on median of
lies on median of ![]() and divide it in ratio 2 : 1.
and divide it in ratio 2 : 1.
Point ![]() lies on Euler line of
lies on Euler line of ![]()
According the Claim, ![]()
![]()
Similarly ![]()
Case 2 Obtuse triangle
a) It is known, that Euler line of obtuse ![]() cross AC and BC (middle and longest sides) in inner points.
cross AC and BC (middle and longest sides) in inner points.
Let ![]() be circumcenters of
be circumcenters of ![]()
Let ![]() and
and ![]() be centroids of
be centroids of ![]()
Denote ![]()
![]() is the circle
is the circle ![]() (the nine-points circle).
(the nine-points circle).
![]() is the midpoint
is the midpoint ![]() where
where ![]() is the orthocenter of
is the orthocenter of ![]()
Similarly ![]()
![]() is the midline of
is the midline of ![]()
Let ![]() cross
cross ![]() at point
at point ![]() different from
different from ![]()
![]() spiral similarity centered at
spiral similarity centered at ![]() maps
maps ![]() onto
onto ![]()
This similarity has the rotation angle ![]() acute angle between Euler lines of these triangles is
acute angle between Euler lines of these triangles is ![]()
Let these lines crossed at point ![]() Therefore
Therefore ![]() points
points ![]() and
and ![]() are concyclic
are concyclic ![]()
Similarly, ![]() as desired.
as desired.
b) ![]()
![]()
Point ![]() lies on median of
lies on median of ![]() and divide it in ratio
and divide it in ratio ![]()
Point ![]() lies on Euler line of
lies on Euler line of ![]() According the Claim,
According the Claim, ![]()
![]()
Similarly ![]()
Claim (Segment crossing the median)
Let ![]() be the midpoint of side
be the midpoint of side ![]() of the
of the ![]()
![]()
![]()
Then ![]()
Proof
Let ![]() be
be ![]() (We use sign
(We use sign ![]() to denote the area of
to denote the area of ![]()
Denote ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Schiffler point
Let ![]() and
and ![]() be the incenter, circumcenter, centroid, circumradius,
be the incenter, circumcenter, centroid, circumradius, ![]() and inradius of
and inradius of ![]() respectively. Then the Euler lines of the four triangles
respectively. Then the Euler lines of the four triangles ![]() and
and ![]() are concurrent at Schiffler point
are concurrent at Schiffler point ![]() .
.
Proof
We will prove that the Euler line ![]() of
of ![]() cross the Euler line
cross the Euler line ![]() of
of ![]() at such point
at such point ![]() that
that ![]() .
.
Let ![]() and
and ![]() be the circumcenter and centroid of
be the circumcenter and centroid of ![]() respectively.
respectively.
It is known that ![]() lies on circumcircle of
lies on circumcircle of ![]()
Denote ![]()
It is known that ![]() is midpoint
is midpoint ![]() point
point ![]() lies on median
lies on median ![]() points
points ![]() belong the bisector of
belong the bisector of ![]()
Easy to find that ![]() ,
,
![]()
We use sigh [t] for area of t. We get
![]()
![]()
![]() Using Claim we get
Using Claim we get
![]() Therefore each Euler line of triangles
Therefore each Euler line of triangles ![]() cross Euler line of
cross Euler line of ![]() in the same point, as desired.
in the same point, as desired.
Claim (Segments crossing inside triangle)
Given triangle GOY. Point ![]() lies on
lies on ![]()
Point ![]() lies on
lies on ![]()
Point ![]() lies on
lies on ![]()
Point ![]() lies on
lies on ![]() Then
Then ![]()
Proof
Let ![]() be
be ![]() (We use sigh
(We use sigh ![]() for area of
for area of ![]()
![]()
![]()
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Euler line as radical axis
Let ![]() with altitudes
with altitudes ![]() and
and ![]() be given.
be given.
Let ![]() and
and ![]() be circumcircle, circumcenter, orthocenter and circumradius of
be circumcircle, circumcenter, orthocenter and circumradius of ![]() respectively.
respectively.
Circle ![]() centered at
centered at ![]() passes through
passes through ![]() and is tangent to the radius AO. Similarly define circles
and is tangent to the radius AO. Similarly define circles ![]() and
and ![]()
Then Euler line of ![]() is the radical axis of these circles.
is the radical axis of these circles.
If ![]() is acute, then these three circles intersect at two points located on the Euler line of the
is acute, then these three circles intersect at two points located on the Euler line of the ![]()
Proof
The power of point ![]() with respect to
with respect to ![]() and
and ![]() is
is ![]()
The power of point ![]() with respect to
with respect to ![]() is
is ![]()
The power of point ![]() with respect to
with respect to ![]() is
is ![]()
The power of point ![]() with respect to
with respect to ![]() is
is ![]()
It is known that ![]()
Therefore points ![]() and
and ![]() lies on radical axis of these three circles as desired.
lies on radical axis of these three circles as desired.
vladimir.shelomovskii@gmail.com, vvsss
De Longchamps point X(20)
Definition 1
The De Longchamps’ point of a triangle is the radical center of the power circles of the triangle. Prove that De Longchamps point lies on Euler line.
We call A-power circle of a ![]() the circle centered at the midpoint
the circle centered at the midpoint ![]() point
point ![]() with radius
with radius ![]() The other two circles are defined symmetrically.
The other two circles are defined symmetrically.
Proof
Let ![]() and
and ![]() be orthocenter, circumcenter, and De Longchamps point, respectively.
be orthocenter, circumcenter, and De Longchamps point, respectively.
Denote ![]() power circle by
power circle by ![]() power circle by
power circle by ![]()
![]() WLOG,
WLOG, ![]()
Denote ![]() the projection of point
the projection of point ![]() on
on ![]()
We will prove that radical axes of ![]() power and
power and ![]() power cicles is symmetric to altitude
power cicles is symmetric to altitude ![]() with respect
with respect ![]() Further, we will conclude that the point of intersection of the radical axes, symmetrical to the heights with respect to O, is symmetrical to the point of intersection of the heights
Further, we will conclude that the point of intersection of the radical axes, symmetrical to the heights with respect to O, is symmetrical to the point of intersection of the heights ![]() with respect to
with respect to ![]()
Point ![]() is the crosspoint of the center line of the
is the crosspoint of the center line of the ![]() power and
power and ![]() power circles and there radical axis.
power circles and there radical axis. ![]() We use claim and get:
We use claim and get:
![]()
![]() and
and ![]() are the medians, so
are the medians, so
![]()
We use Claim some times and get:
![]()
![]() radical axes of
radical axes of ![]() power and
power and ![]() power cicles is symmetric to altitude
power cicles is symmetric to altitude ![]() with respect
with respect ![]()
Similarly radical axes of ![]() power and
power and ![]() power cicles is symmetric to altitude
power cicles is symmetric to altitude ![]() radical axes of
radical axes of ![]() power and
power and ![]() power cicles is symmetric to altitude
power cicles is symmetric to altitude ![]() with respect
with respect ![]() Therefore the point
Therefore the point ![]() of intersection of the radical axes, symmetrical to the heights with respect to
of intersection of the radical axes, symmetrical to the heights with respect to ![]() is symmetrical to the point
is symmetrical to the point ![]() of intersection of the heights with respect to
of intersection of the heights with respect to ![]() lies on Euler line of
lies on Euler line of ![]()
Claim (Distance between projections)
![]()
![]()
![]()
Definition 2
We call ![]() circle of a
circle of a ![]() the circle centered at
the circle centered at ![]() with radius
with radius ![]() The other two circles are defined symmetrically. The De Longchamps point of a triangle is the radical center of
The other two circles are defined symmetrically. The De Longchamps point of a triangle is the radical center of ![]() circle,
circle, ![]() circle, and
circle, and ![]() circle of the triangle (Casey – 1886). Prove that De Longchamps point under this definition is the same as point under Definition 1.
circle of the triangle (Casey – 1886). Prove that De Longchamps point under this definition is the same as point under Definition 1.
Proof
Let ![]() and
and ![]() be orthocenter, centroid, and De Longchamps point, respectively. Let
be orthocenter, centroid, and De Longchamps point, respectively. Let ![]() cross
cross ![]() at points
at points ![]() and
and ![]() The other points
The other points ![]() are defined symmetrically.
are defined symmetrically.
![]()
![]() Similarly
Similarly ![]() is diameter
is diameter ![]()
![]()
Therefore ![]() is anticomplementary triangle of
is anticomplementary triangle of ![]() is orthic triangle of
is orthic triangle of ![]() So
So ![]() is orthocenter of
is orthocenter of ![]()
![]() as desired.
as desired.
vladimir.shelomovskii@gmail.com, vvsss
De Longchamps line
The de Longchamps line ![]() of
of ![]() is defined as the radical axes of the de Longchamps circle
is defined as the radical axes of the de Longchamps circle ![]() and of the circumscribed circle
and of the circumscribed circle ![]() of
of ![]()
Let ![]() be the circumcircle of
be the circumcircle of ![]() (the anticomplementary triangle of
(the anticomplementary triangle of ![]()
Let ![]() be the circle centered at
be the circle centered at ![]() (centroid of
(centroid of ![]() ) with radius
) with radius ![]() where
where ![]()
Prove that the de Longchamps line is perpendicular to Euler line and is the radical axes of ![]() and
and ![]()
Proof
Center of ![]() is
is ![]() , center of
, center of ![]() is
is ![]() where
where ![]() is Euler line.
The homothety with center
is Euler line.
The homothety with center ![]() and ratio
and ratio ![]() maps
maps ![]() into
into ![]() This homothety maps
This homothety maps ![]() into
into ![]()
![]() and
and ![]() there is two inversion which swap
there is two inversion which swap ![]() and
and ![]()
First inversion ![]() centered at point
centered at point ![]() Let
Let ![]() be the point of crossing
be the point of crossing ![]() and
and ![]()
The radius of ![]() we can find using
we can find using ![]()
![]()
![]()
Second inversion ![]() centered at point
centered at point ![]() We can make the same calculations and get
We can make the same calculations and get ![]() as desired.
as desired.
vladimir.shelomovskii@gmail.com, vvsss
CIRCUMCENTER OF THE TANGENTIAL TRIANGLE X(26)
Prove that the circumcenter of the tangential triangle ![]() of
of ![]() (Kimberling’s point
(Kimberling’s point ![]() lies on the Euler line of
lies on the Euler line of ![]()
Proof
Let ![]() and
and ![]() be midpoints of
be midpoints of ![]() and
and ![]() respectively.
respectively.
Let ![]() be circumcircle of
be circumcircle of ![]() It is nine-points circle of the
It is nine-points circle of the ![]()
Let ![]() be circumcircle of
be circumcircle of ![]() Let
Let ![]() be circumcircle of
be circumcircle of ![]()
![]() and
and ![]() are tangents to
are tangents to ![]() inversion with respect
inversion with respect ![]() swap
swap ![]() and
and ![]() Similarly, this inversion swap
Similarly, this inversion swap ![]() and
and ![]() and
and ![]() Therefore this inversion swap
Therefore this inversion swap ![]() and
and ![]()
The center ![]() of
of ![]() and the center
and the center ![]() of
of ![]() lies on Euler line, so the center
lies on Euler line, so the center ![]() of
of ![]() lies on this line, as desired.
lies on this line, as desired.
After some calculations one can find position of point ![]() on Euler line (see Kimberling's point
on Euler line (see Kimberling's point ![]()
vladimir.shelomovskii@gmail.com, vvsss
PERSPECTOR OF ORTHIC AND TANGENTIAL TRIANGLES X(25)
Let ![]() be the orthic triangle of
be the orthic triangle of ![]() Let
Let ![]() be the circumcenter of
be the circumcenter of ![]() Let
Let ![]() be the tangencial triangle of
be the tangencial triangle of ![]() Let
Let ![]() be the circumcenter of
be the circumcenter of ![]()
Prove that lines ![]() and
and ![]() are concurrent at point, lies on Euler line of
are concurrent at point, lies on Euler line of ![]()
Proof
![]() and
and ![]() are antiparallel to BC with respect
are antiparallel to BC with respect ![]()
Similarly, ![]()
Therefore ![]() homothetic center of
homothetic center of ![]() and
and ![]() is the point of concurrence of lines
is the point of concurrence of lines ![]() and
and ![]() Denote this point as
Denote this point as ![]()
The points ![]() and
and ![]() are the corresponding points (circumcenters) of
are the corresponding points (circumcenters) of ![]() and
and ![]() so point
so point ![]() lies on line
lies on line ![]()
Points ![]() and
and ![]() lies on Euler line, so
lies on Euler line, so ![]() lies on Euler line of
lies on Euler line of ![]()
vladimir.shelomovskii@gmail.com, vvsss
Exeter point X(22)
Exeter point is the perspector of the circummedial triangle ![]() and the tangential triangle
and the tangential triangle ![]() By another words, let
By another words, let ![]() be the reference triangle (other than a right triangle). Let the medians through the vertices
be the reference triangle (other than a right triangle). Let the medians through the vertices ![]() meet the circumcircle
meet the circumcircle ![]() of triangle
of triangle ![]() at
at ![]() and
and ![]() respectively. Let
respectively. Let ![]() be the triangle formed by the tangents at
be the triangle formed by the tangents at ![]() and
and ![]() to
to ![]() (Let
(Let ![]() be the vertex opposite to the side formed by the tangent at the vertex A). Prove that the lines through
be the vertex opposite to the side formed by the tangent at the vertex A). Prove that the lines through ![]() and
and ![]() are concurrent, the point of concurrence lies on Euler line of triangle
are concurrent, the point of concurrence lies on Euler line of triangle ![]() the point of concurrence
the point of concurrence ![]() lies on Euler line of triangle
lies on Euler line of triangle ![]() where
where ![]() - circumcenter,
- circumcenter, ![]() - orthocenter,
- orthocenter, ![]() - circumradius.
- circumradius.
Proof
At first we prove that lines ![]() and
and ![]() are concurrent. This follows from the fact that lines
are concurrent. This follows from the fact that lines ![]() and
and ![]() are concurrent at point
are concurrent at point ![]() and Mapping theorem.
and Mapping theorem.
Let ![]() and
and ![]() be the midpoints of
be the midpoints of ![]() and
and ![]() respectively. The points
respectively. The points ![]() and
and ![]() are collinear. Similarly the points
are collinear. Similarly the points ![]() and
and ![]() are collinear.
are collinear.
Denote ![]() the inversion with respect
the inversion with respect ![]() It is evident that
It is evident that ![]()
Denote ![]()
![]()
The power of point ![]() with respect
with respect ![]() is
is ![]()
Similarly the power of point ![]() with respect
with respect ![]() is
is ![]()
![]() lies on radical axis of
lies on radical axis of ![]() and
and ![]()
Therefore second crosspoint of ![]() and
and ![]() point
point ![]() lies on line
lies on line ![]() which is the Euler line of
which is the Euler line of ![]() Point
Point ![]() lies on the same Euler line as desired.
lies on the same Euler line as desired.
Last we will find the length of ![]()
![]()
![]()
![]()
![]()
![]() as desired.
as desired.
Mapping theorem
Let triangle ![]() and incircle
and incircle ![]() be given.
be given.
![]() Let
Let ![]() be the point in the plane
be the point in the plane ![]() Let lines
Let lines ![]() and
and ![]() crossing
crossing ![]() second time at points
second time at points ![]() and
and ![]() respectively.
respectively.
Prove that lines ![]() and
and ![]() are concurrent.
are concurrent.
Proof
![]() We use Claim and get:
We use Claim and get: ![]()
![]() Similarly,
Similarly, ![]()
We use the trigonometric form of Ceva's Theorem for point ![]() and triangle
and triangle ![]() and get
and get
![]() We use the trigonometric form of Ceva's Theorem for triangle
We use the trigonometric form of Ceva's Theorem for triangle ![]() and finish proof that lines
and finish proof that lines ![]() and
and ![]() are concurrent.
are concurrent.
Claim (Point on incircle)
Let triangle ![]() and incircle
and incircle ![]() be given.
be given.
![]()
![]() Prove that
Prove that ![]()
Proof
![]()
![]()
![]()
Similarly ![]()
We multiply and divide these equations and get:
![]()
vladimir.shelomovskii@gmail.com, vvsss
Far-out point X(23)
Let ![]() be the tangential triangle of
be the tangential triangle of ![]()
Let ![]() and
and ![]() be the centroid, circumcircle, circumcenter, circumradius and orthocenter of
be the centroid, circumcircle, circumcenter, circumradius and orthocenter of ![]()
Prove that the second crosspoint of circumcircles of ![]() and
and ![]() is point
is point ![]() Point
Point ![]() lies on Euler line of
lies on Euler line of ![]()
Proof
Denote ![]() the inversion with respect
the inversion with respect ![]() midpoints of
midpoints of ![]()
It is evident that ![]()
The inversion of circles ![]() are lines
are lines ![]() which crosses at point
which crosses at point ![]()
Therefore point ![]() lies on Euler line
lies on Euler line ![]() of
of ![]() as desired.
as desired.
vladimir.shelomovskii@gmail.com, vvsss
Symmetric lines
Let triangle ![]() having the circumcircle
having the circumcircle ![]() be given.
be given.
Prove that the lines symmetric to the Euler line with respect ![]() and
and ![]() are concurrent and the point of concurrence lies on
are concurrent and the point of concurrence lies on ![]()
Proof
The orthocenter ![]() lies on the Euler line therefore the Euler line is
lies on the Euler line therefore the Euler line is ![]() We use H-line Clime and finish the proof.
We use H-line Clime and finish the proof.
H–line Claim
Let triangle ![]() having the orthocenter
having the orthocenter ![]() and circumcircle
and circumcircle ![]() be given. Denote
be given. Denote ![]() any line containing point
any line containing point ![]()
Let ![]() and
and ![]() be the lines symmetric to
be the lines symmetric to ![]() with respect
with respect ![]() and
and ![]() respectively.
respectively.
Prove that ![]() and
and ![]() are concurrent and the point of concurrence lies on
are concurrent and the point of concurrence lies on ![]()
Proof
Let ![]() and
and ![]() be the crosspoints of
be the crosspoints of ![]() with
with ![]() and
and ![]() respectively.
respectively.
WLOG ![]() Let
Let ![]() and
and ![]() be the points symmetric to
be the points symmetric to ![]() with respect
with respect ![]() and
and ![]() respectively.
respectively.
Therefore ![]()
![]()
Let ![]() be the crosspoint of
be the crosspoint of ![]() and
and ![]() is cyclic
is cyclic ![]()
Similarly ![]() is cyclic
is cyclic ![]() the crosspoint of
the crosspoint of ![]() and
and ![]() is point
is point ![]()
vladimir.shelomovskii@gmail.com, vvsss
See also
- Kimberling center
- Kimberling’s point X(20)
- Kimberling’s point X(21)
- Kimberling’s point X(22)
- Kimberling’s point X(23)
- Kimberling’s point X(24)
- Kimberling’s point X(25)
- Kimberling’s point X(26)
- De Longchamps point
- Gossard perspector
- Evans point
- Double perspective triangles
- Steiner line
- Miquel's point
- Spieker center
- Simson line
- Complete Quadrilateral
- Gauss line
- Isogonal conjugate
- Barycentric coordinates
- Symmetry
- Symmedian and Antiparallel
- Central line
- Gergonne line
- Gergonne point
This article is a stub. Help us out by expanding it.