Difference between revisions of "2021 AMC 12A Problems/Problem 23"

Revision as of 23:09, 31 October 2022

The following problem is from both the 2021 AMC 10A #23 and 2021 AMC 12A #23, so both problems redirect to this page.

1 Problem
2 Solution 1
3 Solution 2 (Complementary Counting)
4 Solution 3 (Direct Counting and Probability States)
5 Solution 4 (Finds Numerator and Denominator Separately)
6 Solution 5
7 Solution 6
8 Solution 7 (Casework)
9 Solution 8
10 Solution 9 (Markov Chain)
11 Video Solution by Punxsutawney Phil
12 Video Solution by OmegaLearn (Using Probability States)
13 Video Solution by TheBeautyofMath
14 Video Solution by TheCALT (Casework)
15 Video Solution by MRENTHUSIASM (English & Chinese)
16 Video Solution by firebolt360
17 See also

Problem

Frieda the frog begins a sequence of hops on a $3 \times 3$ grid of squares, moving one square on each hop and choosing at random the direction of each hop-up, down, left, or right. She does not hop diagonally. When the direction of a hop would take Frieda off the grid, she "wraps around" and jumps to the opposite edge. For example if Frieda begins in the center square and makes two hops "up", the first hop would place her in the top row middle square, and the second hop would cause Frieda to jump to the opposite edge, landing in the bottom row middle square. Suppose Frieda starts from the center square, makes at most four hops at random, and stops hopping if she lands on a corner square. What is the probability that she reaches a corner square on one of the four hops?

$\textbf{(A)} ~\frac{9}{16}\qquad\textbf{(B)} ~\frac{5}{8}\qquad\textbf{(C)} ~\frac{3}{4}\qquad\textbf{(D)} ~\frac{25}{32}\qquad\textbf{(E)} ~\frac{13}{16}$

Solution 1

Let us go through the frog’s jumps step by step to find the probability that it will land in a corner. Denote the frog’s position as F:

$[asy] dot((0,0)); draw((-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle); draw((2,-1)--(2,1)--(4,1)--(4,-1)--cycle); draw((-1,2)--(-1,4)--(1,4)--(1,2)--cycle); draw((-1,-4)--(-1,-2)--(1,-2)--(1,-4)--cycle); draw((-4,2)--(-2,2)--(-2,4)--(-4,4)--cycle); draw((4,-2)--(2,-2)--(2,-4)--(4,-4)--cycle); draw((4,2)--(2,2)--(2,4)--(4,4)--cycle); draw((-4,-2)--(-2,-2)--(-2,-4)--(-4,-4)--cycle); draw((-4,0)--(4,0)); draw((0,4)--(0,-4)); draw((-3,-3)--(3,-3)--(3,3)--(-3,3)--cycle); [/asy]$

First notice that since the frog only moves up, down, left or right, it’s original hop will not matter by symmetry, because all first hops will bring the frog at the edge next to two corners. ~KingRavi

Solution 2 (Complementary Counting)

We will use complementary counting. First, the frog can go left with probability $\frac14$ . We observe symmetry, so our final answer will be multiplied by 4 for the 4 directions, and since $4\cdot \frac14=1$ , we will ignore the leading probability.

From the left, she either goes left to another edge ( $\frac14$ ) or back to the center ( $\frac14$ ). Time for some casework.

$\textbf{Case 1:}$ She goes back to the center.

Now, she can go in any 4 directions, and then has 2 options from that edge. This gives $\frac12$ . --End case 1

$\textbf{Case 2:}$ She goes to another edge (rightmost).

Subcase 1: She goes back to the left edge. She now has 2 places to go, giving $\frac12$

Subcase 2: She goes to the center. Now any move works.

$\frac14 \cdot \frac12 + \frac14 \cdot 1=\frac18 + \frac 14=\frac38$ for this case. --End case 2

She goes back to the center in Case 1 with probability $\frac14$ , and to the right edge with probability $\frac14$

So, our answer is $\frac14 \cdot \frac12 + \frac14 \cdot \frac38=\frac14 (\frac12+\frac38)=\frac14 \cdot \frac78 = \frac7{32}$

But, don't forget complementary counting. So, we get $1-\frac7{32}=\frac{25}{32} \implies \boxed{D}$ . ~ firebolt360

Solution 3 (Direct Counting and Probability States)

We can draw a state diagram with three states: center, edge, and corner. Denote center by M, edge by E, and corner by C. There are a few ways Frieda can reach a corner in four or less moves: EC, EEC, EEEC, EMEC. Then, calculating the probabilities of each of these cases happening, we have $1\cdot\tfrac{1}{2}+1\cdot\tfrac{1}{4}\cdot\tfrac{1}{2}+1\cdot\tfrac{1}{4}\cdot\tfrac{1}{4}\cdot\tfrac{1}{2}+1\cdot\tfrac{1}{4}\cdot1\cdot\tfrac{1}{2}=\tfrac{25}{32}$ , so the answer is $\boxed{D}$ . ~IceWolf10

Solution 4 (Finds Numerator and Denominator Separately)

Suppose Frieda makes four independent hops without stopping so that each outcome is equally likely.

Denominator

There are $4^4=256$ ways for Frieda to make four hops without restrictions.

Numerator

We perform casework on which hop Frieda reaches a corner for the first time:

The second hop (The third and the fourth hops have no restrictions.)

The four hops have $4, 2, 4, 4$ options, respectively. So, this case has $4\cdot2\cdot4\cdot4=128$ ways.

The third hop (The fourth hop has no restrictions.)

No matter which direction the first hop takes, the second hop must "wrap around".

The four hops have $4, 1, 2, 4$ options, respectively. So, this case has $4\cdot1\cdot2\cdot4=32$ ways.

The fourth hop (There are two subcases based on the second hop.)

The second hop "wraps around". It follows that the third hop must also "wrap around".

The four hops have $4, 1, 1, 2$ options, respectively. So, this subcase has $4\cdot1\cdot1\cdot2=8$ ways.

The second hop returns to the center.

The four hops have $4, 1, 4, 2$ options, respectively. So, this subcase has $4\cdot1\cdot4\cdot2=32$ ways.

Together, this case has $8+32=40$ ways.

The numerator is $128+32+40=200.$

Probability

The requested probability is $\frac{200}{256}=\boxed{\textbf{(D)} ~\frac{25}{32}}.$

Remark

This problem is quite similar to 1995 AIME Problem 3.

~MRENTHUSIASM

Solution 5

Let $C_n$ be the probability that Frieda is on the central square after n moves, $E_n$ be the probability that Frieda is on one of the four squares on the middle of the edges after n moves, and $V_n$ (V for vertex) be the probability that Frieda is on a corner after n moves. The only way to reach the center is by moving in $1$ specific direction out of $4$ total directions from the middle of an edge, so $C_{n+1}=\frac{E_n}{4}$ . The ways to reach the middle of an edge are by moving in any direction from the center or by moving in $1$ specific direction from the middle of an edge, so $E_{n+1}=C_n+\frac{E_n}{4}$ . The ways to reach a corner are by simply staying there after reaching there in a previous move or by moving in $2$ specific directions from the middle of an edge, so $V_{n+1}=V_n+\frac{E_n}{2}$ . Since Frieda always start from the center, $C_0=1$ , $E_0=0$ , and $V_0=0$ . We use the previous formulas to work out $V_4$ and find it to be $\boxed{\textbf{(D)} ~\frac{25}{32}}$ .

-SmileKat32

Solution 6

Imagine an infinite grid of $2$ by $2$ squares such that there is a $2$ by $2$ square centered at $(3x, 3y)$ for all ordered pairs of integers $(x, y).$

$[asy] dot((0,0)); draw((-1,-1)--(-1,1)--(1,1)--(1,-1)--cycle); draw((-4,-1)--(-4,1)--(-2,1)--(-2,-1)--cycle); draw((2,-1)--(2,1)--(4,1)--(4,-1)--cycle); draw((-1,2)--(-1,4)--(1,4)--(1,2)--cycle); draw((-1,-4)--(-1,-2)--(1,-2)--(1,-4)--cycle); draw((-4,2)--(-2,2)--(-2,4)--(-4,4)--cycle); draw((4,-2)--(2,-2)--(2,-4)--(4,-4)--cycle); draw((4,2)--(2,2)--(2,4)--(4,4)--cycle); draw((-4,-2)--(-2,-2)--(-2,-4)--(-4,-4)--cycle); draw((-3,-3)--(3,-3)--(3,3)--(-3,3)--cycle); draw((-4,0)--(4,0)); draw((0,4)--(0,-4)); [/asy]$

It is easy to see that the problem is equivalent to Frieda moving left, right, up, or down on this infinite grid starting at $(0, 0)$ . (minus the teleportations) Since counting the complement set is easier, we'll count the number of $4$ -step paths such that Frieda never reaches a corner point.

In other words, since the reachable corner points are $(\pm 1, \pm 1), (\pm 1, \pm 2), (\pm 2, \pm 1),$ and $(\pm 2, \pm 2),$ Frieda can only travel along the collection of points included in $S$ , where $S$ is all points on $x=0$ and $y=0$ such that $|y|<4$ and $|x|<4$ , respectively, plus all points on the big square with side length $6$ centered at $(0, 0).$ We then can proceed with casework:

Case $1$ : Frieda never reaches $(0, \pm 3)$ nor $(\pm 3, 0).$

When Frieda only moves horizontally or vertically for her four moves, she can do so in $2^4 - 4 = 12$ ways for each case . Thus, $12 \cdot 2$ total paths for the subcase of staying in one direction. (For instance, all length $4$ combinations of $F$ and $B$ except $FFFF$ , $BBBB$ , $FFFB$ , and $BBBF$ for the horizontal direction.)

There is another subcase where she changes directions during her path. There are four symmetric cases for this subcase depending on which of the four quadrants Frieda hugs. For the first quadrant, the possible paths are $FBUD$ , $FBUU$ , $UDFB$ , and $UDFF.$ Thus, a total of $4 \cdot 4 = 16$ ways for this subcase.

Total for Case $1$ : $24 + 16 = 40$

Case $2$ : Frieda reaches $(0, \pm 3)$ or $(\pm 3, 0)$ .

Once Frieda reaches one of the points listed above (by using three moves), she has four choices for her last move. Thus, a total of $4 \cdot 4 = 16$ paths for this case.

Our total number of paths never reaching coroners is thus $16+40=56,$ making for an answer of $\frac{4^4-56}{4^4} = \boxed{\textbf{(D)} ~\frac{25}{32}}.$

-fidgetboss_4000

Solution 7 (Casework)

We take cases on the number of hops needed to reach a corner. For simplicity, denote $E$ as a move that takes Frieda to an edge, $W$ as wrap-around move and $C$ as a corner move. Also, denote $O$ as a move that takes us to the center.

2 Hops

Then, Frieda will have to $(E, C)$ as her set of moves. There are $4$ ways to move to an edge, and $2$ corners to move to, for a total of $4 \cdot 2 = 8$ cases here. Then, there are $4$ choices for each move, for a probability of $\frac{8}{4 \cdot 4} = \frac{1}{2}$ .

3 Hops

In this case, Frieda must wrap-around. There's only one possible combination, just $(E, W, C)$ . There are $4$ ways to move to an edge, $1$ way to wrap-around (you must continue in the same direction) and $2$ corners, for a total of $4 \cdot 1 \cdot 2 = 8$ cases here. Then, there are $4$ choices for each move, for a probability of $\frac{8}{4 \cdot 4 \cdot 4} = \frac{1}{8}$ .

4 Hops

Lastly, there are two cases we must consider here. The first case is $(E, O, E, C)$ , and the second is $(E, W, W, C)$ . For the first case, there are $4$ ways to move to an edge, $1$ way to return to the center, $4$ ways to move to an edge once again, and $2$ ways to move to a corner. Hence, there is a total of $4 \cdot 1 \cdot 4 \cdot 2 = 32$ cases here. Then, for the second case, there are $4$ ways to move to a corner, $1$ way to wrap-around, $1$ way to wrap-around again, and $2$ ways to move to a corner. This implies there are $4 \cdot 1 \cdot 1 \cdot 2 = 8$ cases here. Then, there is a total of $8+32 = 40$ cases, out of a total of $4^4 = 256$ cases, for a probability of $\frac{40}{256} = \frac{5}{32}$ .

Then, the total probability that Frieda ends up on a corner is $\frac{1}{2} + \frac{1}{8} + \frac{5}{32} = \frac{25}{32}$ , corresponding to choice $\boxed{\textbf{(D)} ~\frac{25}{32}}$ . ~rocketsri

Solution 8

I denote 3x3 grid by

- HOME square (x1)

- CORN squares (x4)

- SIDE squares (x4)

Transitions:

- HOME always move to SIDE

- CORN is DONE

- SIDE move to HOME with $p=1/4,$ move to SIDE with $p=1/4,$ and move to CORN with $p=1/2.$

After one move, will be on $\text{SIDE}$ square

After two moves, will be $1/2 + 1/4 (\text{HOME}) + 1/4 (\text{SIDE})$

After three moves, will be $1/2 + 1/4 (\text{SIDE}) + 1/4 (1/2 + 1/4(\text{SIDE}) + 1/4(\text{HOME}))$

After four moves, probability on CORN will be $1/2 + 1/4 (1/2) + 1/4( 1/2 + 1/4(1/2)) = 1/2 + 1/8 + 5/32 = 25 / 32.$

~ ccx09

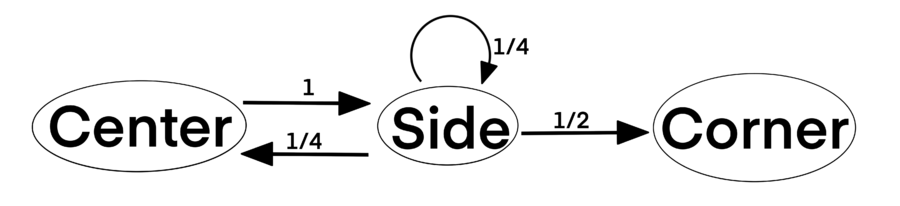
Solution 9 (Markov Chain)

The grid is symmetrical. Denote the center cell as state Center, the $4$ middle side cells as state Side, the $4$ corner cells as state Corner. We can draw the following State Transition Diagram with Markov Chain. The numbers on the transition arc are the transition probability.

We calculate the probability of different states in each round in the following table by iterating a few more times: $\begin{array}{|c|c|c|c|} \hline \textbf{Round} & \textbf{Center} & \textbf{Side} & \textbf{Corner}\\ \hline &&&\\ 1 & 0 & 1 & 0\\ &&&\\ \hline &&&\\ 2 & \frac{1}{4} & \frac{1}{4} & \frac{1}{2}\\ &&&\\ \hline &&&\\ 3 & \frac{1}{4} \cdot \frac{1}{4} = \frac{1}{16} & \frac{1}{4} + \frac{1}{4} \cdot \frac{1}{4} = \frac{5}{16} & \frac{1}{4} \cdot \frac{1}{2} + \frac{1}{2} = \frac{5}{8}\\ &&&\\ \hline &&&\\ 4 & \frac{5}{16} \cdot \frac{1}{4} = \frac{5}{64} & \frac{1}{16} + \frac{5}{16} \cdot \frac{1}{4} = \frac{9}{64} & \frac{5}{16} \cdot \frac{1}{2} + \frac{5}{8} = \frac{25}{32}\\ &&&\\ \hline \end{array}$

Therefore, the answer is $\boxed{\textbf{(D)} ~\frac{25}{32}}$ .

~isabelchen

Video Solution by Punxsutawney Phil

https://youtube.com/watch?v=kHLR57iP0cU

Video Solution by OmegaLearn (Using Probability States)

https://youtu.be/V_Sn30N2q50

~ pi_is_3.14

Video Solution by TheBeautyofMath

https://youtu.be/BM6ttcz8oLA

~IceMatrix

Video Solution by TheCALT (Casework)

https://www.youtube.com/watch?v=BHHZPy9VjAM

~bobthegod78

Video Solution by MRENTHUSIASM (English & Chinese)

https://www.youtube.com/watch?v=f6LrMimIUWw