Y by
Let  be a positive integer. We start with
be a positive integer. We start with  piles of pebbles, each initially containing a single pebble. One can perform moves of the following form: choose two piles, take an equal number of pebbles from each pile and form a new pile out of these pebbles. Find (in terms of
piles of pebbles, each initially containing a single pebble. One can perform moves of the following form: choose two piles, take an equal number of pebbles from each pile and form a new pile out of these pebbles. Find (in terms of  ) the smallest number of nonempty piles that one can obtain by performing a finite sequence of moves of this form.
) the smallest number of nonempty piles that one can obtain by performing a finite sequence of moves of this form.






 We split the solution into three parts.
We split the solution into three parts.
 Now, given
Now, given 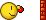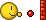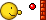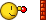 ).
).![\[\begin{cases}
f(n) = 1 & \text{if } n \text{ is a power of } 2 \\
f(n) = 2 & \text{otherwise } \\
\end{cases}\]](http://latex.artofproblemsolving.com/4/5/2/45299fe8b3753a54c6f0a34b811bb01689da13ff.png)
![\[
\boxed{
\begin{cases}
1 & \text{if }n\text{ is a power of }2 \\
2 & \text{otherwise}
\end{cases}
}.
\]](http://latex.artofproblemsolving.com/4/0/0/40017981dd76725e928d63e86594a900c440da62.png)
 .
. where
where  .
.



