2006 AMC 10A Problems
| 2006 AMC 10A (Answer Key) Printable versions: • AoPS Resources • PDF | ||
|
Instructions
| ||
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
Contents
[hide]- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 See also
Problem 1
Sandwiches at Joe's Fast Food cost ![]() each and sodas cost
each and sodas cost ![]() each. How many dollars will it cost to purchase 5 sandwiches and 8 sodas?
each. How many dollars will it cost to purchase 5 sandwiches and 8 sodas?
![]()
Problem 2
Define ![]() . What is
. What is ![]() ?
?
![]()
Problem 3
The ratio of Mary's age to Alice's age is ![]() . Alice is
. Alice is ![]() years old. How many years old is Mary?
years old. How many years old is Mary?
![]()
Problem 4
A digital watch displays hours and minutes with AM and PM. What is the largest possible sum of the digits in the display?
![]()
Problem 5
Doug and Dave shared a pizza with 8 equally-sized slices. Doug wanted a plain pizza, but Dave wanted anchovies on half of the pizza. The cost of a plain pizza was 8 dollars, and there was an additional cost of 2 dollars for putting anchovies on one half. Dave ate all of the slices of anchovy pizza and one plain slice. Doug ate the remainder. Each then paid for what he had eaten. How many more dollars did Dave pay than Doug?
![]()
Problem 6
What non-zero real value for ![]() satisfies
satisfies ![]() ?
?
![]()
Problem 7
![[asy] unitsize(3mm); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=4; draw((0,4)--(18,4)--(18,-4)--(0,-4)--cycle); draw((6,4)--(6,0)--(12,0)--(12,-4)); label("$A$",(0,4),NW); label("$B$",(18,4),NE); label("$C$",(18,-4),SE); label("$D$",(0,-4),SW); label("$y$",(3,4),S); label("$y$",(15,-4),N); label("$18$",(9,4),N); label("$18$",(9,-4),S); label("$8$",(0,0),W); label("$8$",(18,0),E); dot((0,4)); dot((18,4)); dot((18,-4)); dot((0,-4));[/asy]](http://latex.artofproblemsolving.com/6/6/a/66a524a2244d311dbe57cc4d9aaffc1b5e83bb03.png)
The ![]() rectangle
rectangle ![]() is cut into two congruent hexagons, as shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is
is cut into two congruent hexagons, as shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is ![]() ?
?
![]()
Problem 8
A parabola with equation ![]() passes through the points
passes through the points ![]() and
and ![]() . What is
. What is ![]() ?
?
![]()
Problem 9
How many sets of two or more consecutive positive integers have a sum of 15?
![]()
Problem 10
For how many real values of ![]() is
is ![]() an integer?
an integer?
![]()
Problem 11
Which of the following describes the graph of the equation ![]() ?
?
![]()
Problem 12
![[asy] size(150); pathpen = linewidth(0.6); defaultpen(fontsize(10)); D((0,0)--(16,0)--(16,-16)--(0,-16)--cycle); D((16,-8)--(24,-8)); label('Dog', (24, -8), SE); MP('I', (8,-8), (0,0)); MP('8', (16,-4), W); MP('8', (16,-12),W); MP('8', (20,-8), N); label('Rope', (20,-8),S); D((0,-20)--(16,-20)--(16,-36)--(0,-36)--cycle); D((16,-24)--(24,-24)); MP("II", (8,-28), (0,0)); MP('4', (16,-22), W); MP('8', (20,-24), N); label("Dog",(24,-24),SE); label("Rope", (20,-24), S); [/asy]](http://latex.artofproblemsolving.com/6/6/d/66db58ca0de01a6dab5b8ddb18e671f265759bfa.png)
Rolly wishes to secure his dog with an 8-foot rope to a square shed that is 16 feet on each side. His preliminary drawings are shown.
Which of these arrangements give the dog the greater area to roam, and by how many square feet?
![]()
Problem 13
A player pays ![]() to play a game. A die is rolled. If the number on the die is odd, the game is lost. If the number on the die is even, the die is rolled again. In this case the player wins if the second number matches the first and loses otherwise. How much should the player win if the game is fair? (In a fair game the probability of winning times the amount won is what the player should pay.)
to play a game. A die is rolled. If the number on the die is odd, the game is lost. If the number on the die is even, the die is rolled again. In this case the player wins if the second number matches the first and loses otherwise. How much should the player win if the game is fair? (In a fair game the probability of winning times the amount won is what the player should pay.)
![]()
Problem 14
![[asy] size(7cm); pathpen = linewidth(0.7); D(CR((0,0),10)); D(CR((0,0),9.5)); D(CR((0,-18.5),9.5)); D(CR((0,-18.5),9)); MP("$\vdots$",(0,-31),(0,0)); D(CR((0,-39),3)); D(CR((0,-39),2.5)); D(CR((0,-43.5),2.5)); D(CR((0,-43.5),2)); D(CR((0,-47),2)); D(CR((0,-47),1.5)); D(CR((0,-49.5),1.5)); D(CR((0,-49.5),1.0)); D((12,-10)--(12,10)); MP('20',(12,0),E); D((12,-51)--(12,-48)); MP('3',(12,-49.5),E);[/asy]](http://latex.artofproblemsolving.com/7/5/b/75b3e762b96f49323740d90a83fdb1339789180e.png)
A number of linked rings, each 1 cm thick, are hanging on a peg. The top ring has an outside diameter of 20 cm. The outside diameter of each of the other rings is 1 cm less than that of the ring above it. The bottom ring has an outside diameter of 3 cm. What is the distance, in cm, from the top of the top ring to the bottom of the bottom ring?
![]()
Problem 15
Odell and Kershaw run for 30 minutes on a circular track. Odell runs clockwise at 250 m/min and uses the inner lane with a radius of 50 meters. Kershaw runs counterclockwise at 300 m/min and uses the outer lane with a radius of 60 meters, starting on the same radial line as Odell. How many times after the start do they pass each other?
![]()
Problem 16
![[asy] size(200); pathpen = linewidth(0.7); pointpen = black; real t=2^0.5; D((0,0)--(4*t,0)--(2*t,8)--cycle); D(CR((2*t,2),2)); D(CR((2*t,5),1)); D('B', (0,0),SW); D('C',(4*t,0), SE); D('A', (2*t, 8), N); D((2*t,2)--(2*t,4)); D((2*t,5)--(2*t,6)); MP('2', (2*t,3), W); MP('1',(2*t, 5.5), W);[/asy]](http://latex.artofproblemsolving.com/f/4/a/f4a115a9c8dc91a741d0149edb037b3cb07f6b01.png)
A circle of radius 1 is tangent to a circle of radius 2. The sides of ![]() are tangent to the circles as shown, and the sides
are tangent to the circles as shown, and the sides ![]() and
and ![]() are congruent. What is the area of
are congruent. What is the area of ![]() ?
?
![]()
Problem 17
In rectangle ![]() , points
, points ![]() and
and ![]() trisect
trisect ![]() , and points
, and points ![]() and
and ![]() trisect
trisect ![]() . In addition,
. In addition, ![]() , and
, and ![]() . What is the area of quadrilateral
. What is the area of quadrilateral ![]() shown in the figure?
shown in the figure?
![[asy] size(7cm); pathpen = linewidth(0.7); pointpen = black; pointfontpen = fontsize(10); pair A,B,C,D,E,F,G,H,W,X,Y,Z; A=(0,2); B=(1,2); C=(2,2); D=(3,2); H=(0,0); G=(1,0); F=(2,0); E=(3,0); D('A',A, N); D('B',B,N); D('C',C,N); D('D',D,N); D('E',E,SE); D('F',F,SE); D('G',G,SW); D('H',H,SW); D(A--F); D(B--E); D(D--G); D(C--H); Z=IP(A--F, C--H); Y=IP(A--F, D--G); X=IP(B--E,D--G); W=IP(B--E,C--H); D('W',W,1.6*N); D('X',X,1.6*plain.E); D('Y',Y,1.6*S); D('Z',Z,1.6*plain.W); D(A--D--E--H--cycle); [/asy]](http://latex.artofproblemsolving.com/6/1/4/614d325a6be5be041b053c50024bd55a65735595.png)
![]()
Problem 18
A license plate in a certain state consists of 4 digits, not necessarily distinct, and 2 letters, also not necessarily distinct. These six characters may appear in any order, except that the two letters must appear next to each other. How many distinct license plates are possible?
![]()
Problem 19
How many non-similar triangles have angles whose degree measures are distinct positive integers in arithmetic progression?
![]()
Problem 20
Six distinct positive integers are randomly chosen between 1 and 2006, inclusive. What is the probability that some pair of these integers has a difference that is a multiple of 5?
![]()
Problem 21
How many four-digit positive integers have at least one digit that is a ![]() or a
or a ![]() ?
?
![]()
Problem 22
Two farmers agree that pigs are worth $300 and that goats are worth $210. When one farmer owes the other money, he pays the debt in pigs or goats, with "change" received in the form of goats or pigs as necessary. (For example, a $390 debt could be paid with two pigs, with one goat received in change.) What is the amount of the smallest positive debt that can be resolved in this way?
![]()
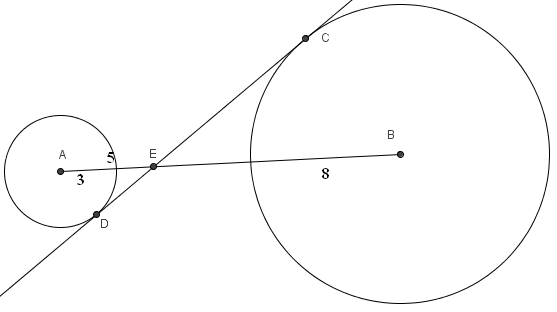
Problem 23
Circles with centers ![]() and
and ![]() have radii
have radii ![]() and
and ![]() , respectively. A common internal tangent intersects the circles at
, respectively. A common internal tangent intersects the circles at ![]() and
and ![]() , respectively. Lines
, respectively. Lines ![]() and
and ![]() intersect at
intersect at ![]() , and
, and ![]() . What is
. What is ![]() ?
?
![]()
Problem 24
Centers of adjacent faces of a unit cube are joined to form a regular octahedron. What is the volume of this octahedron?
![]()
Problem 25
A bug starts at one vertex of a cube and moves along the edges of the cube according to the following rule. At each vertex the bug will choose to travel along one of the three edges emanating from that vertex. Each edge has equal probability of being chosen, and all choices are independent. What is the probability that after seven moves the bug will have visited every vertex exactly once?
![]()
See also
| 2006 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by 2005 AMC 10B Problems |
Followed by 2006 AMC 10B Problems | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
- AMC 10
- AMC 10 Problems and Solutions
- 2006 AMC 10A
- 2006 AMC A Math Jam Transcript
- Mathematics competition resources
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()