2006 AMC 12A Problems/Problem 16
(Redirected from 2006 AMC 10A Problems/Problem 23)
- The following problem is from both the 2006 AMC 12A #16 and 2006 AMC 10A #23, so both problems redirect to this page.
Problem
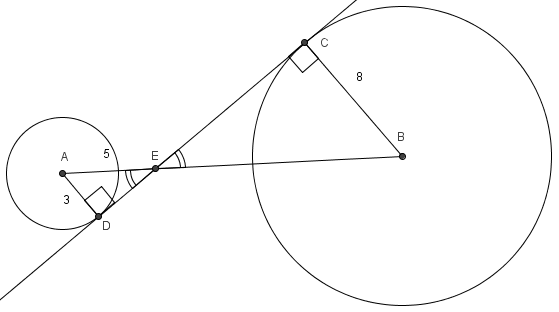
Circles with centers ![]() and
and ![]() have radius 3 and 8, respectively. A common internal tangent intersects the circles at
have radius 3 and 8, respectively. A common internal tangent intersects the circles at ![]() and
and ![]() , respectively. Lines
, respectively. Lines ![]() and
and ![]() intersect at
intersect at ![]() , and
, and ![]() . What is
. What is ![]() ?
?
![[asy] unitsize(2.5mm); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=3; pair A=(0,0), Ep=(5,0), B=(5+40/3,0); pair M=midpoint(A--Ep); pair C=intersectionpoints(Circle(M,2.5),Circle(A,3))[1]; pair D=B+8*dir(180+degrees(C)); dot(A); dot(C); dot(B); dot(D); draw(C--D); draw(A--B); draw(Circle(A,3)); draw(Circle(B,8)); label("$A$",A,W); label("$B$",B,E); label("$C$",C,SE); label("$E$",Ep,SSE); label("$D$",D,NW); [/asy]](http://latex.artofproblemsolving.com/8/9/3/8932f7dfafa96fd7b5e9bd90951c495dea0015fb.png)
![]()
Solution
![]() and
and ![]() are vertical angles so they are congruent, as are angles
are vertical angles so they are congruent, as are angles ![]() and
and ![]() (both are right angles because the radius and tangent line at a point on a circle are always perpendicular). Thus,
(both are right angles because the radius and tangent line at a point on a circle are always perpendicular). Thus, ![]() .
By the Pythagorean Theorem, line segment
.
By the Pythagorean Theorem, line segment ![]() . The sides are proportional, so
. The sides are proportional, so ![]() . This makes
. This makes ![]() and
and ![]() .
.
See also
| 2006 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 15 |
Followed by Problem 17 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
| 2006 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 22 |
Followed by Problem 24 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()