Difference between revisions of "2006 AMC 12A Problems/Problem 6"
I like pie (talk | contribs) (Duplicate, AMC 10 box) |
5849206328x (talk | contribs) m (Minor typo) |
||
| Line 1: | Line 1: | ||
| − | {{duplicate|[[2006 AMC 12A Problems|2006 AMC 12A #6]] and [[2006 AMC 10A Problems/Problem 7| | + | {{duplicate|[[2006 AMC 12A Problems|2006 AMC 12A #6]] and [[2006 AMC 10A Problems/Problem 7|2006 AMC 10A #7]]}} |
== Problem == | == Problem == | ||
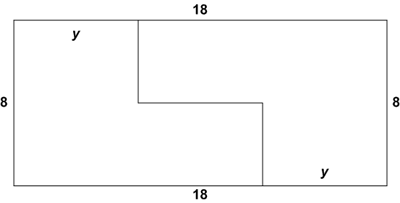
The <math>8\times18</math> [[rectangle]] <math>ABCD</math> is cut into two congruent hexagons, as shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is <math>y</math>? | The <math>8\times18</math> [[rectangle]] <math>ABCD</math> is cut into two congruent hexagons, as shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is <math>y</math>? | ||
Revision as of 22:04, 31 May 2009
- The following problem is from both the 2006 AMC 12A #6 and 2006 AMC 10A #7, so both problems redirect to this page.
Problem
The 
rectangle 
is cut into two congruent hexagons, as shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is 
?
Solution
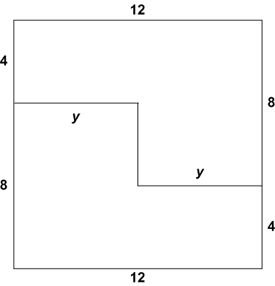
Since the two hexagons are going to be repositioned to form a square without overlap, the area will remain the same. The rectangle's area is 
. This means the square will have four sides of length 12. The only way to do this is shown below.
As you can see from the diagram, the line segment denoted as is half the length of the side of the square, which leads to 
.
See also
| 2006 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 5 |
Followed by Problem 7 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
| 2006 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 6 |
Followed by Problem 8 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
