,
to be the least positive integer for which the following holds:
into 
disjoint subsets 
,
.
for which![\[\deg(P_i(x)-P_j(x))\geq \frac{n}{k}-f(n)\]](http://latex.artofproblemsolving.com/2/0/9/2092eb944c746d1449e7865f9da4e0065b75bdef.png)
so that 
for all 
.
and circumcircle 
.
and 
,
be the circumcenter of 
,
intersects 
and the line through 
meet on 
and the domain 
passing through the origin touch 
.
be a mobile point on the parabola 
the distances between the point 
on a coordinate plane such that for all points 
over the domain 
holds.
be the open unit disk in the complex plane and let 
be a holomorphic function such that 
.
be 
.
.
we have the inequality 
,
,
(where the sum has 
is the order of the quotient group 
(the index of the subgroup 
)
![$\{x_n\} \subseteq [0,1]$](http://latex.artofproblemsolving.com/8/e/4/8e4206325387485d73765c9d7070ecb1ce18ff60.png)
,
,
and 
could be chosen to satisfy 
and 
.
Such That 
is even?
Then 
But I am stuck. I came across this functional equation by trying to find a limit of a sequence, I can show that if it is helpful. 
has solutio
satisfy 
for all 
.
be a fixed circle, and let 
be a point outside 
.
and 
,
is cyclic, where 
are fixed points on the circle.
,
,
is the tangent from 
is the point of tangency.
,
,
is perpendicular to chord 
.
and 
lie on a circle, their cross-ratio is harmonic:![\[
(ANMB) = -1.
\]](http://latex.artofproblemsolving.com/b/d/5/bd5301ba76f493aec0821c454dffc46dea93c0f2.png)
- The intersection points 
,
![\[y''+by'+cy=g(t)\]](http://latex.artofproblemsolving.com/7/8/8/7882dc954ab6dba2445b68d370d630ce1c66a6db.png)
with 
,
are constants has the form ![\[y(t)=\int^{t}_{t_0}K(t-s)g(s)ds\,\]](http://latex.artofproblemsolving.com/6/3/c/63c34df1c0013bf659bc76506a93873a5f879070.png)
and use variation of parameters in each case to find the solution. Is there any short way to calculate solution?
that exist function 
such 
and discontinuous on 
Y by Miku_, tiendung2006, son7, ImSh95, Rounak_iitr, Tastymooncake2, ItsBesi
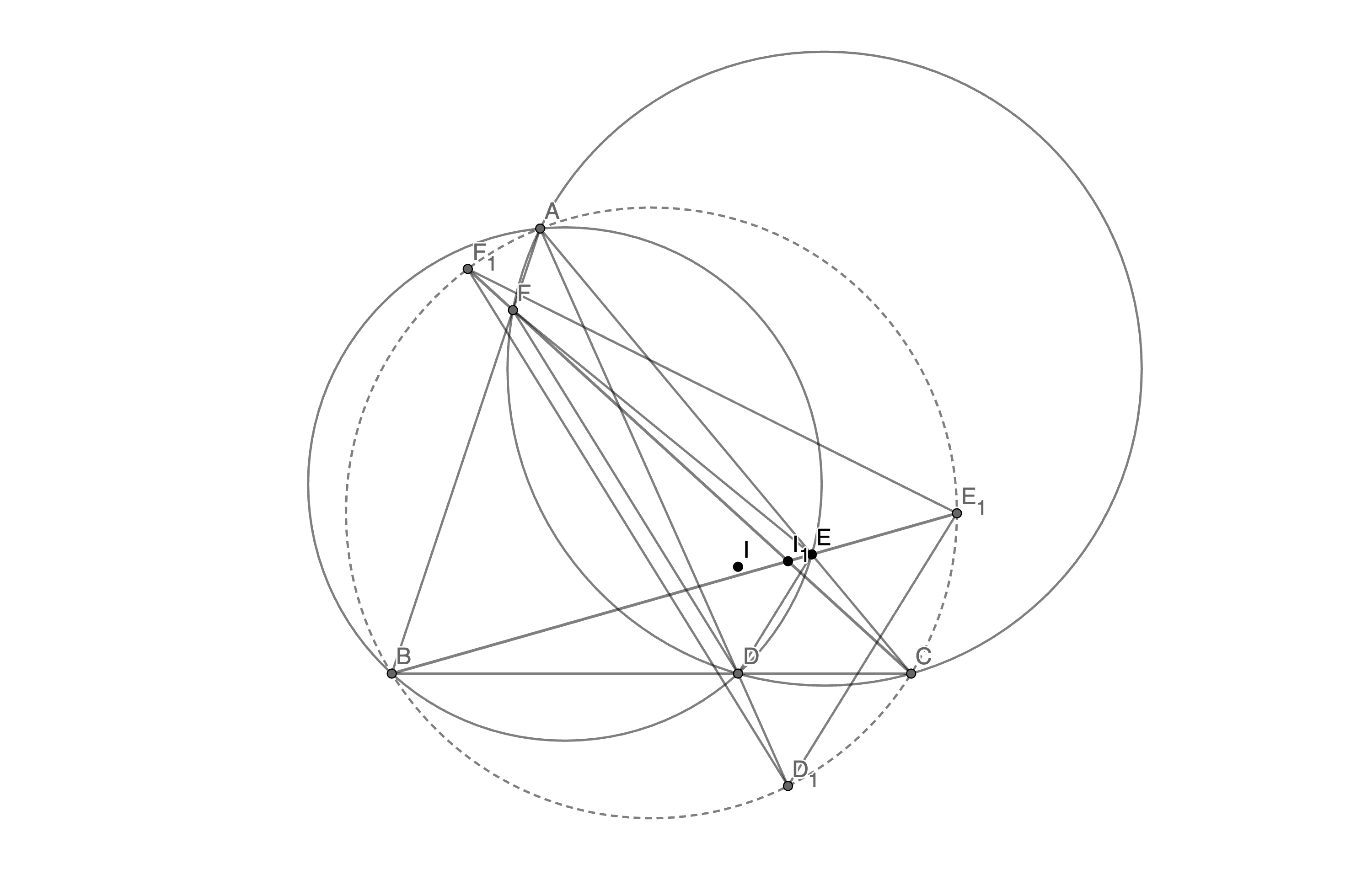
Let 
be an interior point on the side 
of an acute-angled triangle 
. Let the circumcircle of triangle 
intersect 
again at 
and the circumcircle of triangle 
intersect 
again at 
. Let 
, 
, and 
intersect the circumcircle of triangle again at 
, 
and 
, respectively. Let 
and 
be the incentres of triangles 
and 
, respectively. Prove that 
are concyclic.
be an interior point on the side 
of an acute-angled triangle 
. Let the circumcircle of triangle 
intersect 
again at 
and the circumcircle of triangle 
intersect 
again at 
. Let 
, 
, and 
intersect the circumcircle of triangle again at 
, 
and 
, respectively. Let 
and 
be the incentres of triangles 
and 
, respectively. Prove that 
are concyclic.
and 
are angle bisectors in 
(infact the corresponding lines are parallel).
in 
,
because 
as 
and similarly 
.
with incenter 
,
.
using the two given cyclites, then using that 
and 
giving the desired cyclicity. 
lie inside 
as 
,
and 
and 
are bisectors of 
when 
Similarly 
[This part was motivated by ELMOSL 2013 G3]
Finally 
we are done 
when we use 
.
and 
and ![\[\measuredangle F_1D_1A = \measuredangle F_1CA = \measuredangle FCA = \measuredangle FDA \implies DF \parallel D_1F_1\]](http://latex.artofproblemsolving.com/6/3/0/63043bb9aa76eb8aa1ffc4e7cf75652280cd3da3.png)
One can analogously chase to prove that other pair of lines are parallel as well. Now, we show that 
bisects angle ![\[\measuredangle CF_1E_1 = \measuredangle CBE_1 = \measuredangle DBE =\measuredangle DAE = \measuredangle D_1AC = \measuredangle D_1F_1C\]](http://latex.artofproblemsolving.com/1/e/3/1e3f2ec5f27637bc651a374b270701d48772d7cd.png)
and the other one follows symmetrically. 
.![\[\angle F_1I_1E_1 = \angle FI_1E = \angle 90^\circ + \frac{\angle F_1D_1E_1}{2} = \angle FIE \implies \angle EI_1F = \angle EIF\]](http://latex.artofproblemsolving.com/0/2/7/0270347485696e845f6d2e4eb152f17519816ca7.png)
and thus we are done. 
is concyclic. Notice that
and 
implies that 
and 
are similar. So
So B is the midpoint of arc 
that doesn't contain 
.
.So, 
and 
due to the bisectors. So,
are concyclic and thus I lies in the circle as proved before and the claim is proved
by a simple angle chase.
is its miquel point.
we get that quadrilateral 
must be cyclic.Now its well known that if 
is the centre of 
,
(
)
bisects 
(
)
.
is angle bisector of 
.
is angle bisector of 
.
.
.
which implies 
is cyclic.
,
,
.
and 
are collinear. By symnmetry, it suffices to show that 
bisects 
.
,
.
as 
by Reim's theorem and similar.
is cyclic.
,
,![\[\angle EIF = 90 + \frac{\angle EDF}{2} = 90 + \frac{180-2\angle A}{2} = 180-\angle A.\]](http://latex.artofproblemsolving.com/3/8/9/389ff50445471886794f149f11748bae8f55e348.png)
is 
,![\[\angle D_1E_1B = \angle DAF = \angle DCF = \angle BE_1F_1.\]](http://latex.artofproblemsolving.com/4/5/3/453c0193f23cc75824d90f50e4fcfe8bafa291eb.png)
Similarily, the angle bisector 
.
and that 
and now it is trivial to see the required result.
similarly we get 
similarly we get 
be the intersection of 
are simmilar 
combining with 
we get that triangles 
are also simmilar 
is the angle bisector of 
i
hence 
we get that quadrilaterals 
and 
are cyclic 
By Miquel Theorem that the quadrilateral 
is also cyclic
which means that 
is cyclic hence 
is cyclic
you solve this problem and you are 
but 
implies 
so 
which finishes.
![[asy]
import graph; size(28.259587460059326cm); real lsf=0.5; pen dps=linewidth(0.7)+fontsize(10); defaultpen(dps); pen ds=black; real xmin=-3.647195849593462,xmax=24.612391610465863,ymin=-7.509267023422269,ymax=5.573532154808459;
pen qqwuqq=rgb(0.,0.39215686274509803,0.);
pair A=(7.04,2.68), B=(5.56,-2.08), C=(11.84,-1.9), D=(8.406260425428417,-1.9984192871692494), F=(6.625518995492593,1.3469394719896899), E_1=(11.51418510673573,1.598202569865462), F_1=(5.933180208263576,1.7780431876423513), D_1=(8.968848272394865,-3.9248615561455518), I=(8.352856644003863,-0.13522069080146587), I_1=(8.857582314416177,-0.04291591111145887);
draw(A--B--C--cycle,linewidth(2.)+red); draw(D_1--E_1--F_1--cycle,linewidth(2.)+qqwuqq); draw(D--(9.486520842231533,0.34561136303741335)--F--cycle,linewidth(2.)+blue);
draw(A--B,linewidth(2.)+red); draw(B--C,linewidth(2.)+red); draw(C--A,linewidth(2.)+red); draw(circle((6.9216226068641475,0.10672238273971847),2.575999010616734),linewidth(2.)); draw(circle((8.655353603542784,-0.4323368347149838),3.5065663885348504),linewidth(2.)); draw(circle((10.03811586962979,1.0168463262495604),3.4285243050378944),linewidth(2.)); draw(D_1--E_1,linewidth(2.)+qqwuqq); draw(E_1--F_1,linewidth(2.)+qqwuqq); draw(F_1--D_1,linewidth(2.)+qqwuqq); draw(circle((8.30438487295115,1.5559055437042604),1.6918207510320091),linewidth(2.)+linetype("4 4")); draw(D--(9.486520842231533,0.34561136303741335),linewidth(2.)+blue); draw((9.486520842231533,0.34561136303741335)--F,linewidth(2.)+blue); draw(F--D,linewidth(2.)+blue); draw(B--E_1,linewidth(2.)); draw(C--F_1,linewidth(2.)); draw(A--D_1,linewidth(2.));
dot(A,ds); label("$A$",(7.119243700763566,2.8680241094519623),NE*lsf); dot(B,ds); label("$B$",(5.451464768694492,-2.5429919812610295),NE*lsf); dot(C,ds); label("$C$",(11.714901202465018,-1.709102515226493),NE*lsf); dot(D,ds); label("$D$",(8.24962719916594,-2.48739935019206),NE*lsf); dot((9.486520842231533,0.34561136303741335),linewidth(4.pt)+ds); label("$E$",(9.63944297589017,0.19957781814144593),NE*lsf); dot(F,linewidth(4.pt)+ds); label("$F$",(6.693033529234802,1.4967392097507248),NE*lsf); dot(E_1,linewidth(4.pt)+ds); label("$E_1$",(11.51106155521213,1.9600111353254672),NE*lsf); dot(F_1,linewidth(4.pt)+ds); label("$F_1$",(5.710897047016347,2.0156037663944364),NE*lsf); dot(D_1,linewidth(4.pt)+ds); label("$D_1$",(9.102047542223467,-4.247832667376081),NE*lsf); dot(I,linewidth(4.pt)+ds); label("$I$",(8.286688953211918,-0.02279270613443046),NE*lsf); dot(I_1,linewidth(4.pt)+ds); label("$I_1$",(8.8611461409246,0.1810469411184562),NE*lsf);
clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle);
[/asy]](http://latex.artofproblemsolving.com/5/3/0/53049f0832c742fef05d53268bca8a70fa0a2f79.png)
are concyclic
as required.
and 
intersect at 
is the angle bisector, similarly, 
is the other angle bisector and they intersect at 
