2008 iTest Problems/Problem 96
Contents
[hide]Problem
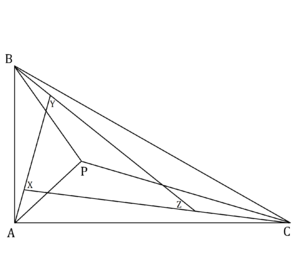
Triangle ![]() has
has ![]() , and
, and ![]() , and a point
, and a point ![]() is chosen inside the triangle. The interior angle bisectors
is chosen inside the triangle. The interior angle bisectors ![]() , and
, and ![]() of respective angles
of respective angles ![]() , and
, and ![]() intersect pairwise at
intersect pairwise at ![]() , and
, and ![]() . If triangles
. If triangles ![]() and
and ![]() are directly similar, then the area of
are directly similar, then the area of ![]() may be written in the form
may be written in the form ![]() , where
, where![]() are positive integers,
are positive integers, ![]() and
and ![]() are not divisible by the square of any prime, and
are not divisible by the square of any prime, and ![]() . Compute
. Compute ![]() .
.
Solution
Let ![]() . With some angle chasing, we find that
. With some angle chasing, we find that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
By using 30-60-90 triangles, we find that ![]() and
and ![]() . By the Law of Sines on
. By the Law of Sines on ![]() and
and ![]() ,
, ![]() and
and ![]() . After solving for
. After solving for ![]() in both equations, we have
in both equations, we have
 Thus, by using identities,
Thus, by using identities,  . Now we will determine the length of
. Now we will determine the length of ![]() . We will only substitute
. We will only substitute ![]() at the very end (along with the other trigonometric expressions) to keep calculations simple.
at the very end (along with the other trigonometric expressions) to keep calculations simple.
Using the definition of a cosine, we have ![]() . By the Law of Sines on
. By the Law of Sines on ![]() ,
, ![]() , so
, so ![]() . Thus
. Thus ![]() .
.
We know that the area of ![]() is
is ![]() and that
and that ![]() Therefore,
Therefore,
![\begin{align*} [XYZ] &= 32\sqrt{3} \cdot \frac{64 \cdot 3 \cos^2 (x) - 16 \cdot 32\sqrt{3} \sin(x) \cos(x) + 32^2 \sin^2 (x)}{64 \cdot 3} \\ &= \sqrt{3} \left( \frac{96 \cos^2 (x) - 256\sqrt{3} \sin(x) \cos(x) + 32 \cdot 16 \sin^2 (x)}{3} \right) \\ &= 16\sqrt{3} \left( \frac{26 \sin^2 (x) - 8\sqrt{3} \sin(2x) + 6}{3} \right) \\ &= 16\sqrt{3} \left( \frac{26(\frac{19-4\sqrt{19}}{38}) - 8\sqrt{3} \frac{\sqrt{3}}{\sqrt{19}} + 6}{3} \right) \\ &= \frac{16\sqrt{3}}{3} \left( 13 - \frac{52\sqrt{19}}{19} - \frac{24\sqrt{19}}{19} + 6 \right) \\ &= \frac{16\sqrt{3}}{3} ( 19 - 4\sqrt{19} ) \\ &= \frac{304\sqrt{3} - 64\sqrt{57}}{3} \end{align*}](http://latex.artofproblemsolving.com/3/8/0/380d23334c4f63ef0c3ed9839a3011b0071ab26a.png) Therefore,
Therefore, ![]() .
.
Note
The original problem says that ![]() , and
, and ![]() . This is a typo.
. This is a typo.
See Also
| 2008 iTest (Problems) | ||
| Preceded by: Problem 95 |
Followed by: Problem 97 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 • 31 • 32 • 33 • 34 • 35 • 36 • 37 • 38 • 39 • 40 • 41 • 42 • 43 • 44 • 45 • 46 • 47 • 48 • 49 • 50 • 51 • 52 • 53 • 54 • 55 • 56 • 57 • 58 • 59 • 60 • 61 • 62 • 63 • 64 • 65 • 66 • 67 • 68 • 69 • 70 • 71 • 72 • 73 • 74 • 75 • 76 • 77 • 78 • 79 • 80 • 81 • 82 • 83 • 84 • 85 • 86 • 87 • 88 • 89 • 90 • 91 • 92 • 93 • 94 • 95 • 96 • 97 • 98 • 99 • 100 | ||