2008 iTest Problems/Problem 98
Problem
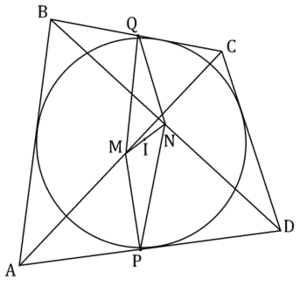
Convex quadrilateral ![]() has side-lengths
has side-lengths ![]() ,
, ![]() ,
, ![]() , and there exists a circle, lying inside the quadrilateral and having center
, and there exists a circle, lying inside the quadrilateral and having center ![]() , that is tangent to all four sides of the quadrilateral. Points
, that is tangent to all four sides of the quadrilateral. Points ![]() and
and ![]() are on the midpoints of
are on the midpoints of ![]() and
and ![]() respectively. It can be proven that point
respectively. It can be proven that point ![]() always lies on segment
always lies on segment ![]() . Supposing further that
. Supposing further that ![]() is the midpoint of
is the midpoint of ![]() , the area of quadrilateral
, the area of quadrilateral ![]() may be expressed as
may be expressed as ![]() , where
, where ![]() and
and ![]() are positive integers and
are positive integers and ![]() is not divisible by the square of any prime. Compute
is not divisible by the square of any prime. Compute ![]() .
.
Solution (credit to official solution)
Let ![]() be the midpoint of
be the midpoint of ![]() and
and ![]() be the midpoint of
be the midpoint of ![]() . Draw lines from
. Draw lines from ![]() and
and ![]() to
to ![]() and
and ![]() , as seen in the diagram. By SAS Similarity, we find that
, as seen in the diagram. By SAS Similarity, we find that ![]() and
and ![]() , so
, so ![]() . Similarly,
. Similarly, ![]() .
.
Because opposite sides of ![]() have equal length,
have equal length, ![]() is a parallelogram. Thus, the diagonals bisect each other, and
is a parallelogram. Thus, the diagonals bisect each other, and ![]() .
.
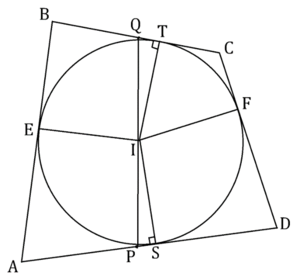
Let ![]() be on
be on ![]() where
where ![]() , and let
, and let ![]() be on
be on ![]() where
where ![]() . Also, let
. Also, let ![]() be on
be on ![]() where
where ![]() , and let
, and let ![]() be on
be on ![]() where
where ![]() . By HL Congruency,
. By HL Congruency, ![]() , so
, so ![]() . Now we have information we can use to determine side lengths to compute the inradius so we can determine the area of
. Now we have information we can use to determine side lengths to compute the inradius so we can determine the area of ![]() .
.
Let ![]() . That means
. That means ![]() ,
, ![]() , and
, and ![]() . That means
. That means ![]() . Additionally, since
. Additionally, since ![]() and
and ![]() ,
, ![]() and
and ![]() . Since
. Since ![]() , we must have
, we must have ![]() .
.
We know that ![]() , so
, so
 Let
Let ![]() be the radius of the incircle. That means
be the radius of the incircle. That means
 Therefore, the area of the quadrilateral is
Therefore, the area of the quadrilateral is ![]() , so
, so ![]() .
.
See Also
| 2008 iTest (Problems) | ||
| Preceded by: Problem 97 |
Followed by: Problem 99 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 • 31 • 32 • 33 • 34 • 35 • 36 • 37 • 38 • 39 • 40 • 41 • 42 • 43 • 44 • 45 • 46 • 47 • 48 • 49 • 50 • 51 • 52 • 53 • 54 • 55 • 56 • 57 • 58 • 59 • 60 • 61 • 62 • 63 • 64 • 65 • 66 • 67 • 68 • 69 • 70 • 71 • 72 • 73 • 74 • 75 • 76 • 77 • 78 • 79 • 80 • 81 • 82 • 83 • 84 • 85 • 86 • 87 • 88 • 89 • 90 • 91 • 92 • 93 • 94 • 95 • 96 • 97 • 98 • 99 • 100 | ||