Homothecy
 by rrusczyk, Jun 17, 2006, 3:21 PM
by rrusczyk, Jun 17, 2006, 3:21 PM
The first class I'll be teaching in WOOT involves using basic tools to solve advanced geometry problems. The three main tools are similar triangles, power of a point, and cyclic quadrilaterals. At least one of these tools is a key step in the solution to most Olympiad geometry problems. In fact, many advanced geometry tools are essentially extensions of these basic tools. One example is homothecy.
Two figures are said to be homothetic if one is essentially a blown up version of the other. (You may also have learned this as a 'dilation'.)
Below is an example of a pair of figures which illustrate homothecy.
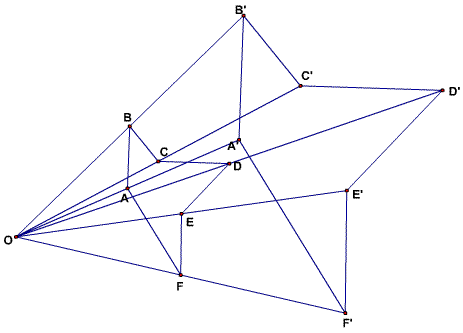
A homothecy with center O maps every point X of a figure to a point Y such that O, X, Y are collinear and OX = k(OY) for a fixed constant k. (In other words, the vector OY is k times the vector OX.)
For example, two equilateral triangles which have the same orientation are homothetic:
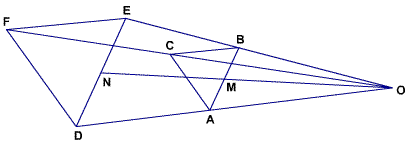
Note in the diagram that every line through corresponding parts of the two triangles also passes through O. Specifically, the line through A and D (corresponding vertices) goes through O, as does the line through B and E, and the line through C and F. The line through M, the midpoint of AB, and N, the midpoint of DE, also goes through O, as these are corresponding parts of the triangle as well. Therefore, homothecy can sometimes be used for collinearity and concurrency problems.
Some properties of homothecy which are useful in problems (and you can assume to be true unless you're specifically asked to prove them) are:
If segments AB and XY are homothetic, then AB and XY are parallel. (Same goes for rays and lines.)
Homothetic figures are similar, with a ratio equal to that of the homothecy ratio k that maps one figure to the other.
Homothetic angles are equal.
Homothecy preserves tangency (i.e. if line m is tangent to circle A, then line m' is tangent to circle A', where m' and A' are homothetic to m,A).
These are all fairly 'obvious' results - you should take the time to prove some of them to see how they nearly all result from basic triangle similarity. (In fact, homothecy is largely just a set of tools that all follow from triangle similarity; most homothecy problems can be tackled with triangle similarity and plenty of work rather than simply invoking homothecy.)
You may invoke all the above statements regarding homothetic figures when you are writing a solution for, say, the USAMO. You just note that two figures are homothetic, and away you go.
Before we dive into problems, note that the homothecy constant ratio need not be positive:
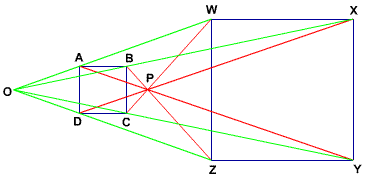
In the diagram, ABCD can be mapped to WXYZ by either the green homothecy with center O, or the red homothecy with center P. The green homothecy maps points in the obvious way A -> W, B -> X, C -> Y, D -> Z, and our ratio is positive.
The red homothecy maps A to a point on the opposite side from P as A (namely, point Y), so the ratio is negative, since the vector PA is in the opposite direction as vector PY.
Some tips to look for homothecy as approach to solving problems are: tangent circles (homothetic with point of tangency as center of homothecy), common tangents to circles (the common external tangents to two circles meet at the center of a homothecy which maps one circle to the other - same for the common internal tangents), and similar figures with parallel corresponding sides. One very common example of this last instance is the homothecy mapping a triangle to its medial triangle (formed by connecting the midpoints of the sides of the original triangle).
Here are a couple examples.
First, from the Mandelbrot Competition:
Two circles are internally tangent at point A. The larger circle has radius 3 and the smaller circle has radius 1. Find the maximum area of a triangle which has the point of tangency as a vertex and one vertex on each of the small and large circles.
Click for solution
For our second example:
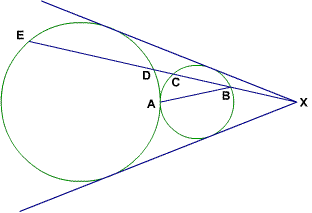
Two circles are externally tangent at A. A line passing through the intersection point of their common external tangents meets the circles at B, C, D, and E as shown. Prove that BA is perpendicular AD.
Click for solution
You'll sometimes see homothecy spelled homothety, as in these excellent links from cut-the-knot below:
http://www.cut-the-knot.com/Curriculum/Geometry/Homothety.shtml
http://www.cut-the-knot.com/Curriculum/Geometry/IncircleInSegment1.shtml
http://www.cut-the-knot.org/ctk/SixCircum2.shtml
Keep investigating the cut-the-knot site; your explorations there of homothecy should bring you to inversion - a topic for some other day. For those who want to get started now:
http://www.cut-the-knot.org/ctk/Circle.shtml
Two figures are said to be homothetic if one is essentially a blown up version of the other. (You may also have learned this as a 'dilation'.)
Below is an example of a pair of figures which illustrate homothecy.

A homothecy with center O maps every point X of a figure to a point Y such that O, X, Y are collinear and OX = k(OY) for a fixed constant k. (In other words, the vector OY is k times the vector OX.)
For example, two equilateral triangles which have the same orientation are homothetic:

Note in the diagram that every line through corresponding parts of the two triangles also passes through O. Specifically, the line through A and D (corresponding vertices) goes through O, as does the line through B and E, and the line through C and F. The line through M, the midpoint of AB, and N, the midpoint of DE, also goes through O, as these are corresponding parts of the triangle as well. Therefore, homothecy can sometimes be used for collinearity and concurrency problems.
Some properties of homothecy which are useful in problems (and you can assume to be true unless you're specifically asked to prove them) are:
If segments AB and XY are homothetic, then AB and XY are parallel. (Same goes for rays and lines.)
Homothetic figures are similar, with a ratio equal to that of the homothecy ratio k that maps one figure to the other.
Homothetic angles are equal.
Homothecy preserves tangency (i.e. if line m is tangent to circle A, then line m' is tangent to circle A', where m' and A' are homothetic to m,A).
These are all fairly 'obvious' results - you should take the time to prove some of them to see how they nearly all result from basic triangle similarity. (In fact, homothecy is largely just a set of tools that all follow from triangle similarity; most homothecy problems can be tackled with triangle similarity and plenty of work rather than simply invoking homothecy.)
You may invoke all the above statements regarding homothetic figures when you are writing a solution for, say, the USAMO. You just note that two figures are homothetic, and away you go.
Before we dive into problems, note that the homothecy constant ratio need not be positive:

In the diagram, ABCD can be mapped to WXYZ by either the green homothecy with center O, or the red homothecy with center P. The green homothecy maps points in the obvious way A -> W, B -> X, C -> Y, D -> Z, and our ratio is positive.
The red homothecy maps A to a point on the opposite side from P as A (namely, point Y), so the ratio is negative, since the vector PA is in the opposite direction as vector PY.
Some tips to look for homothecy as approach to solving problems are: tangent circles (homothetic with point of tangency as center of homothecy), common tangents to circles (the common external tangents to two circles meet at the center of a homothecy which maps one circle to the other - same for the common internal tangents), and similar figures with parallel corresponding sides. One very common example of this last instance is the homothecy mapping a triangle to its medial triangle (formed by connecting the midpoints of the sides of the original triangle).
Here are a couple examples.
First, from the Mandelbrot Competition:
Two circles are internally tangent at point A. The larger circle has radius 3 and the smaller circle has radius 1. Find the maximum area of a triangle which has the point of tangency as a vertex and one vertex on each of the small and large circles.
Click for solution
There might be an inelegant approach with trig and calculus, or plenty of algebra, but homothecy gives us a quick solution. The tangent circles make us think of the homothecy. We extend side AB as shown below, to hit the large circle again at X.
![[asy]
// image with two circles, points A, B, X, and line through A, B, X.
dotfactor = 4;
pair A,B, O_2,C,X, O_1;
A=(-3,0); O_2=(-2,0); O_1=(0,0);
X=(3/2, 3*sqrt(3)/2); C=(3/2, -3*sqrt(3)/2); B=(-3/2, sqrt(3)/2);
draw(Circle(O_1,3));
draw(Circle(O_2,1));
label("$A$",A,W);
dot(O_1); dot(O_2);
draw(A--X); label("$B$",B,N); label("$X$",X,NE);
[/asy]](//latex.artofproblemsolving.com/6/e/2/6e217cb7d85061547741dcb4128297b8484ce0f0.png)
Since the circles are homothetic with center A, we have AB/AX = 1/3. This is true no matter which point B we choose on the smaller circle. Since the ratio of the areas of ABC and AXC is just AB/AX, this means the area of ABC is always 1/3 the area of the corresponding AXC. Therefore, if we maximize the area of triangle AXC, we maximize the area of ABC.
We know how to maximize AXC - we make it equilateral! The area of an equilateral triangle inscribed in a circle with radius 3 is , so the area of our maximal ABC is
, so the area of our maximal ABC is  . The resulting triangle looks like this:
. The resulting triangle looks like this:
![[asy]
// image with two circles, points A, B, X, C, line through A, B, X,
// and triangle AXC drawn in.
dotfactor = 4;
pair A,B, O_2,C,X, O_1;
A=(-3,0); O_2=(-2,0); O_1=(0,0);
X=(3/2, 3*sqrt(3)/2); C=(3/2, -3*sqrt(3)/2); B=(-3/2, sqrt(3)/2);
draw(Circle(O_1,3));
draw(Circle(O_2,1));
label("$A$",A,W);
dot(O_1); dot(O_2);
draw(A--X--C--cycle); label("$B$",B,N); label("$X$",X,NE); label("$C$",C,SE);
[/asy]](//latex.artofproblemsolving.com/0/5/2/052928a5c343fd9f9934224cfd377abad1ba25f1.png)
![[asy]
// image with two circles, points A, B, X, and line through A, B, X.
dotfactor = 4;
pair A,B, O_2,C,X, O_1;
A=(-3,0); O_2=(-2,0); O_1=(0,0);
X=(3/2, 3*sqrt(3)/2); C=(3/2, -3*sqrt(3)/2); B=(-3/2, sqrt(3)/2);
draw(Circle(O_1,3));
draw(Circle(O_2,1));
label("$A$",A,W);
dot(O_1); dot(O_2);
draw(A--X); label("$B$",B,N); label("$X$",X,NE);
[/asy]](http://latex.artofproblemsolving.com/6/e/2/6e217cb7d85061547741dcb4128297b8484ce0f0.png)
Since the circles are homothetic with center A, we have AB/AX = 1/3. This is true no matter which point B we choose on the smaller circle. Since the ratio of the areas of ABC and AXC is just AB/AX, this means the area of ABC is always 1/3 the area of the corresponding AXC. Therefore, if we maximize the area of triangle AXC, we maximize the area of ABC.
We know how to maximize AXC - we make it equilateral! The area of an equilateral triangle inscribed in a circle with radius 3 is
![[asy]
// image with two circles, points A, B, X, C, line through A, B, X,
// and triangle AXC drawn in.
dotfactor = 4;
pair A,B, O_2,C,X, O_1;
A=(-3,0); O_2=(-2,0); O_1=(0,0);
X=(3/2, 3*sqrt(3)/2); C=(3/2, -3*sqrt(3)/2); B=(-3/2, sqrt(3)/2);
draw(Circle(O_1,3));
draw(Circle(O_2,1));
label("$A$",A,W);
dot(O_1); dot(O_2);
draw(A--X--C--cycle); label("$B$",B,N); label("$X$",X,NE); label("$C$",C,SE);
[/asy]](http://latex.artofproblemsolving.com/0/5/2/052928a5c343fd9f9934224cfd377abad1ba25f1.png)
For our second example:
Two circles are externally tangent at A. A line passing through the intersection point of their common external tangents meets the circles at B, C, D, and E as shown. Prove that BA is perpendicular AD.

Click for solution
We have two tips to consider homothecy - the common external tangents and the tangent circles. There's a homothecy with center A that maps the circles to each other, and one with center X. We'll look at the one with center X first, because we have an additional line through X. We let h be the homothecy such that
h(little circle) = h(big circle)
Therefore, h(B) = D and h(C) = E.
At this point, we don't have any information about A, so we draw the line through X and A:
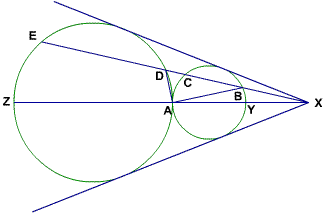
Now we also have h(Y) = A and h(A) = Z.
AY and AZ are diameters of our circles, since AZ connects the point of tangency and the common point of the external tangents (see if you can prove this on your own).
Therefore, is a right angle, as is
is a right angle, as is  . We feel like we're getting close! If only we could show that AD and BY are parallel, we'd be finished. Homothecy does it! Since h(Y) = A and h(B) = D, we have h(YB) = AD, so YB and AD are parallel. Since
. We feel like we're getting close! If only we could show that AD and BY are parallel, we'd be finished. Homothecy does it! Since h(Y) = A and h(B) = D, we have h(YB) = AD, so YB and AD are parallel. Since  is right,
is right,  must be right as well.
must be right as well.
Discovering parallel segments is just one of the powerful uses of homothecy. In our classes, you'll see homothecy used to discover concurrent lines, collinear points, and more.
h(little circle) = h(big circle)
Therefore, h(B) = D and h(C) = E.
At this point, we don't have any information about A, so we draw the line through X and A:

Now we also have h(Y) = A and h(A) = Z.
AY and AZ are diameters of our circles, since AZ connects the point of tangency and the common point of the external tangents (see if you can prove this on your own).
Therefore,
Discovering parallel segments is just one of the powerful uses of homothecy. In our classes, you'll see homothecy used to discover concurrent lines, collinear points, and more.
You'll sometimes see homothecy spelled homothety, as in these excellent links from cut-the-knot below:
http://www.cut-the-knot.com/Curriculum/Geometry/Homothety.shtml
http://www.cut-the-knot.com/Curriculum/Geometry/IncircleInSegment1.shtml
http://www.cut-the-knot.org/ctk/SixCircum2.shtml
Keep investigating the cut-the-knot site; your explorations there of homothecy should bring you to inversion - a topic for some other day. For those who want to get started now:
http://www.cut-the-knot.org/ctk/Circle.shtml
This post has been edited 2 times. Last edited by rrusczyk, Aug 3, 2015, 4:42 PM
Reason: Fix links
Reason: Fix links
 February 2012
February 2012
 January 2012
January 2012